ind the total area covered by two rectilinear rectangles in a 2D plane.
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.

Assume that the total area is never beyond the maximum possible value of int.
Credits:
Special thanks to @mithmatt for adding this problem, creating the above image and all test cases.
解题思路:先判断两矩形是否相交,因为点的坐标相对位置不会发生变化,直接求出相交区域的对角坐标
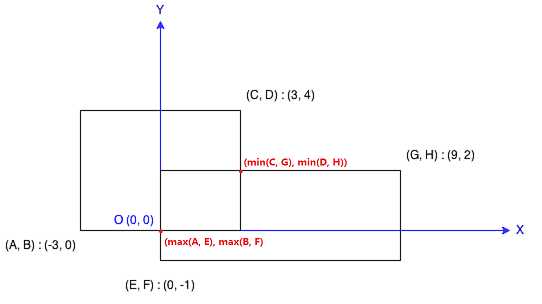
class Solution { public: int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) { int total = (C - A) * (D - B) + (G - E) * (H - F); if(E >= C || A >= G || B >= H || F >= D) return total; return total - (min(C, G) - max(A, E)) * (min(D, H) - max(B, F)); } };
