62. Unique Paths
题目
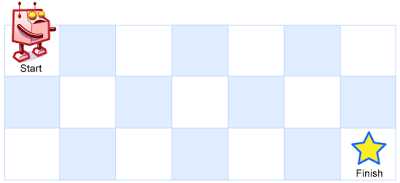
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
解析
class Solution_62 {
public:
int uniquePaths(int m, int n) {
//matrix(m*n)
vector<vector<int>> vecs(m, vector<int>(n, 1));
for (int i = 1; i < m;i++)
{
for (int j = 1; j < n;j++)
{
vecs[i][j] = vecs[i - 1][j] + vecs[i][j - 1];
}
}
return vecs[m-1][n-1];
}
int uniquePaths1(int m, int n) {
vector<int > vec(n, 1); //压缩空间
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (i * j != 0)
vec[j] += vec[j - 1];
return vec[n - 1];
}
// 链接:https://www.nowcoder.com/questionTerminal/166eaff8439d4cd898e3ba933fbc6358
// 动态规划的复杂度也是n方,可以用排列组合的方式,复杂度为n
// 只能向右走或者向下走,所以从一共需要的步数中挑出n - 1个向下走,剩下的m - 1个就是向右走
// 其实就是从(m - 1 + n - 1)里挑选(n - 1)或者(m - 1)个,c(n, r) n = (m - 1 + n - 1), r = (n - 1)
// n!/ (r!* (n - r)!)
//注意观察到,可以发现循环的值是;C(n, m) = n!/ (m!*(n - m)!),因为n值过大,不可以直接用公式
//组合数学的递推公式:C(m,n)=C(m,n-1)+C(m-1,n-1)
//C(n, 1) = n; C(n, n) = 1; C(n, 0) = 1;这样就可以用DP了
int fun(int n, int m)
{
if (m==1)
{
return n;
}
if (n==m||m==0)
{
return 1;
}
return fun(n-1, m ) + fun(n - 1, m - 1); //超时
}
int uniquePaths2(int m, int n) {
n = (m - 1 + n - 1);
m = (m - 1);
int ret=fun(n,m);
return ret;
}
};
解析

