D(树上倍增)
题意:
刚开始有一个点1,权值为0。
接下来有q个操作,每个操作有两种:
1 R W:新加一个点,这个点的权值为W,这个点的父亲是R
2 R X:在从点R到1的路径上,取出从R开始的不降单调栈,问从栈底到栈顶这么多元素,最多能取出多少个点,使得这些点的点权和<=X
强制在线
q<=400000
分析:
虽然这个树的形态不是固定的,但仍旧可以倍增,因为每次加的都是叶子节点,对上面的形态是不改变的
我们可以先倍增求出每个点的最上方的不必它点权小的点fa
然后根据这个fa信息组成一个新的森林,再在这上面倍增去回答点权和<=X的询问

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn=4e5; 5 int fa[maxn+5][20],g[maxn+5][20]; 6 ll mx[maxn+5][20],sum[maxn+5][20]; 7 int dep[maxn+5]; 8 int n; 9 int last=0; 10 int main() 11 { 12 13 int T; 14 scanf("%d",&T); 15 n=1; 16 mx[1][0]=0; 17 dep[1]=1; 18 while(T--) 19 { 20 int op; 21 long long r,w; 22 scanf("%d%lld%lld",&op,&r,&w); 23 24 r^=last,w^=last; 25 //printf("operation : %d %lld %lld\n",op,r,w); 26 if(op==1) 27 { 28 ++n; 29 mx[n][0]=w; 30 fa[n][0]=r; 31 int x=fa[n][0]; 32 for(int i=19;i>=0;--i) 33 if(mx[x][i]<w) x=fa[x][i]; 34 // if(n==3) printf("ce %d\n",x); 35 36 //printf("ce %d %d\n",n,x); 37 for(int i=1;i<=19;++i) 38 { 39 mx[n][i]=max(mx[n][i-1],mx[fa[n][i-1]][i-1]); 40 fa[n][i]=fa[fa[n][i-1]][i-1]; 41 } 42 g[n][0]=x; 43 dep[n]=dep[x]+1; 44 sum[n][0]=w; 45 for(int i=1;i<=19;++i) 46 { 47 sum[n][i]=sum[n][i-1]+sum[g[n][i-1]][i-1]; 48 g[n][i]=g[g[n][i-1]][i-1]; 49 } 50 } 51 else 52 { 53 last=0; 54 int x=r; 55 for(int i=19;i>=0;--i) 56 { 57 //printf("%d : %d ",i,sum[x][i]); 58 if(sum[x][i]<=w) 59 { 60 w-=sum[x][i]; 61 x=g[x][i]; 62 } 63 //printf("%d\n",x); 64 } 65 //printf("x %d\n",x); 66 last=dep[r]-dep[x]; 67 printf("%d\n",last); 68 } 69 } 70 //printf("ce : %d\n",sum[2][0]); 71 return 0; 72 }
E(斯特林数下降幂)
题意:
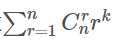
给定n,k,求这个式子的值n<=1e9,k<=5000
分析:
对于x^k这个可以用第二类斯特林数下降幂展开并化简,最后可以得出一个简单的式子
因为k比较小,所以可以直接递推求第二类斯特林数

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int N=5010,P=1e9+7; 5 6 int S[N][N]; 7 8 inline int Pow(int x,int y){ 9 int ret=1; 10 for(;y;y>>=1,x=1LL*x*x%P) if(y&1) ret=1LL*ret*x%P; 11 return ret; 12 } 13 14 inline int A(int n,int j){ 15 int ret=1; 16 for(int i=0;i<j;i++) 17 ret=1LL*ret*(n-i)%P; 18 return ret; 19 } 20 21 int main(){ 22 S[0][0]=1; 23 for(int i=1;i<=5000;i++){ 24 for(int j=1;j<=i;j++) 25 S[i][j]=(S[i-1][j-1]+1LL*j*S[i-1][j])%P; 26 } 27 int ans=0; 28 int n,k; scanf("%d%d",&n,&k); 29 for(int j=1;j<=k && j<=n;j++) 30 ans=(ans+1LL*S[k][j]*A(n,j)%P*Pow(2,n-j))%P; 31 printf("%d\n",ans); 32 return 0; 33 }
F(树上动态凸包)
题意:
有一个n个点的树,每个点有两个属性a和b,对于一个点u,dp[u]=min(dp[v]+a[u]*b[v]),其中v是u子树中的点,求出每个点的dp值
n<=100000
分析:
直接dp肯定会超时
这个如果不是树而是一条链,那是可以用凸包来优化的
如果是一颗树的话,那么自然而然想到就涉及到几个子树的凸包的合并
这个可以采取启发式合并,把小的凸包里的点往大的凸包里的点插,询问就在凸包上二分
凸包用set来维护
注意在set上二分的姿势
时间复杂度O(nlog^2n)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mp make_pair 4 const int maxn=1e5; 5 typedef long long ll; 6 const ll inf=100000000000000000LL; 7 typedef pair<int,ll> Point; 8 ll a[maxn+5],b[maxn+5],dp[maxn+5]; 9 vector<int> g[maxn+5]; 10 int n; 11 set<Point> s[maxn+5]; 12 double cross(Point a,Point b,Point c) 13 { 14 ll x=b.first-a.first,y=b.second-a.second; 15 ll xx=c.first-b.first,yyy=c.second-b.second; 16 return (double)x*yyy-(double)y*xx; 17 } 18 void insert(set<Point> &s,Point p) 19 { 20 set<Point>::iterator it=s.lower_bound(p); 21 set<Point>::iterator jt=it; 22 if(it!=s.begin()) --jt; 23 if(it!=s.begin()&&it!=s.end()&&cross(*jt,p,*it)<=0) return; 24 if(it!=s.begin()) 25 { 26 it=jt; 27 while(it!=s.begin()) 28 { 29 jt=it; 30 --jt; 31 if(cross(*jt,*it,p)<=0) s.erase(it--);else break; 32 } 33 } 34 jt=s.lower_bound(p); 35 if(jt!=s.end()) it=jt++; 36 while(jt!=s.end()) 37 { 38 if(cross(p,*it,*jt)<=0) s.erase(it++);else break; 39 jt=it; 40 ++jt; 41 } 42 s.insert(p); 43 } 44 ll query(set<Point> &s,ll k) 45 { 46 if(s.empty()) return 0; 47 ll l=s.begin()->first,r=s.rbegin()->first,mid; 48 while(l<r) 49 { 50 mid=(l+r+1)>>1; 51 set<Point>::iterator it=s.lower_bound(mp(mid,-inf)),jt=it--; 52 if(k*(jt->first-it->first)>=jt->second-it->second) l=mid;else r=mid-1; 53 } 54 Point res=*s.lower_bound(mp(l,-inf)); 55 return (-k)*res.first+res.second; 56 } 57 void dfs(int k,int fa) 58 { 59 for(auto u:g[k]) 60 { 61 if(u==fa) continue; 62 dfs(u,k); 63 if(s[k].size()<s[u].size()) s[k].swap(s[u]); 64 for(auto x:s[u]) 65 insert(s[k],x); 66 set<Point>().swap(s[u]); 67 } 68 dp[k]=query(s[k],-a[k]); 69 insert(s[k],mp(b[k],dp[k])); 70 71 72 } 73 int main() 74 { 75 scanf("%d",&n); 76 for(int i=1;i<=n;++i) scanf("%lld",&a[i]); 77 for(int i=1;i<=n;++i) scanf("%lld",&b[i]); 78 for(int i=1;i<n;++i) 79 { 80 int u,v; 81 scanf("%d%d",&u,&v); 82 g[u].push_back(v),g[v].push_back(u); 83 } 84 dfs(1,0); 85 for(int i=1;i<=n;++i) printf("%lld ",dp[i]); 86 return 0; 87 }
G(回文树)
待填坑

