题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路:
设前序遍历序列为pre,中序遍历序列为in,则易知:
1)root = pre[0];
2)in[ ] 中 root 的位置(索引)将 in[ ] 分成了root 的左子树和右子树两个部分;
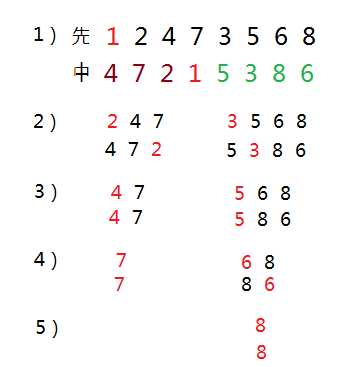
如图所示:先序中的第一个元素就是树的根root 1,在中序中这个根 1 将序列分为了左(4,7,2)、右(5,3,8,6)子树;

递归的看,左子树也有先序(2,4,7)和中序(4,7,2)两个序列,右子树同理;
- c++代码:
1 /** 2 * Definition for binary tree 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) { 13 // 递归退出条件 14 if(pre.size() == 1) { 15 TreeNode *root = new TreeNode(pre[0]); 16 return root; 17 } 18 // 递归退出条件 19 if(pre.size() == 0) { 20 return NULL; 21 } 22 // 中序中root的位置 23 int i; 24 for(i = 0; i < vin.size(); i++) 25 if(vin[i] == pre[0]) 26 break; 27 28 vector<int> inLeft; 29 vector<int> preLeft; 30 vector<int> inRight; 31 vector<int> preRight; 32 // 左子树的先序和中序序列 33 for(int j = 0; j < i; j++) { 34 inLeft.push_back(vin[j]); 35 preLeft.push_back(pre[j+1]); 36 } 37 // 右子树的先序和中序序列 38 for(int j = 0; j < vin.size()-i-1; j++) { 39 inRight.push_back(vin[j+i+1]); 40 preRight.push_back(pre[j+i+1]); 41 } 42 43 TreeNode *root = new TreeNode(pre[0]); 44 root->left = reConstructBinaryTree(preLeft, inLeft); 45 root->right = reConstructBinaryTree(preRight, inRight); 46 47 return root; 48 } 49 };
- java代码:
1 /** 2 * Definition for binary tree 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode(int x) { val = x; } 8 * } 9 */ 10 public class Solution { 11 public TreeNode reConstructBinaryTree(int [] pre,int [] in) { 12 13 // 递归退出条件 14 if(pre.length == 1) { 15 TreeNode root = new TreeNode(pre[0]); 16 return root; 17 } 18 19 // 递归退出条件 20 if(pre.length == 0) 21 return null; 22 23 // 中序中root的索引 24 int i; 25 for(i = 0; i < in.length; i++) 26 if(in[i] == pre[0]) 27 break; 28 29 int [] inLeft = new int[i]; 30 int [] preLeft = new int[i]; 31 int [] inRight = new int[in.length-i-1]; 32 int [] preRight = new int[in.length-i-1]; 33 34 // 左子树的中序和先序序列 35 for(int j = 0; j < i; j++) { 36 inLeft[j] = in[j]; 37 preLeft[j] = pre[j+1]; 38 } 39 40 // 右子树的中序和先序序列 41 for(int j = 0; j < in.length-i-1; j++) { 42 inRight[j] = in[j+i+1]; 43 preRight[j] = pre[j+i+1]; 44 } 45 46 TreeNode root = new TreeNode(pre[0]); 47 root.left = reConstructBinaryTree(preLeft, inLeft); 48 root.right = reConstructBinaryTree(preRight, inRight); 49 50 return root; 51 } 52 }
算法的改进:
- 这种做法每次递归都需要开辟4个数组来保存左、右子树的先、中序列,占用了很多的空间;
- 考虑用把函数的形参换成数组的起始位置,来代替每次传入数组;
