性能评估是用什么样的方法来评估一个模型的预测质量。来对模型的性能进行评价。
回归问题的评估方法
能够想到的评估方法是均方误差:
学习器f,在数据集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_m,y_m)\}$上面的均方误差为 $$E(f;D)= \frac{1}{m} \sum_{i=1}^{m}{(\textbf{x}_i –y_i)}^2$$
分类问题的评估方法
很容易想到的是准确率(accuracy)来进行评估 $准确率=\frac{分类正确的样本数}{总的样本数}$,这个评估方法简单明了,但是只用这一个方法来进行评估有点太单调。不同的任务需要的评价方法不一样,在一个推荐系统当中,为了尽量打扰用户,我们更关心我们预测出来的兴趣当中真正被用户喜欢的概率。在预测罪犯的任务当中,我们更关心的是所有犯罪的人当中全部被我们预测出来的概率,这就是两种不同的评估方法,前者叫做precision(查准率),后者叫做recall(查全率、召回率)。
precision和recall
为了表述分类任务的预测情况,我们需要使用下面的表:
| 预测为正 | 预测为反 | |
| 真正为正 | TP(真正例) | FN(假反例) |
| 真正为反 | FP(假正例) | TN(真反例) |
上面的表叫做混淆矩阵,矩阵里面的值的正例和反例是根据预测结果来决定的,预测为正(Positive),那么结果就是正例,和真实结果相符为真正例(TP),和真实结果相反的为假正例(FP)。 同理预测为反(Negative),有假反例(FN)和真反例(TN)。
在混淆矩阵的基础上我们定义下面两个概念
precision 预测为正的样本当中有多少预测准确了$P = \frac{TP}{TP+FP}$
recall 真正为正的样本当中有多少被预测出来了 $R = \frac{TP}{TP+FN}$
P-R曲线的绘制
查准率和查全率是什么关系哪? 假如我们想要提高查全率,那么我们把所有的样本都预测为正,这个时候我们的准确率势必会下降。很多模型在样本预测的时候并不是单纯的得出一个0,1值,而是得到一个介于0和1之间的小数,然后通过这个数和一个阈值比较(通常为0.5),比这个阈值大的预测为正例,比这个阈值小的预测为反例。 当我们调整这个阈值的时候,我们预测的结果就会改变,所以,绘制P-R曲线的时候是以这个阈值为自变量,阈值改变的时候,查准率和查全率就会改变,将不同的阈值对应的precision和recall的值绘制到图形上面就形成了P-R曲线图。
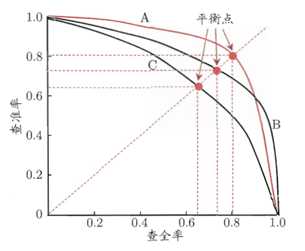
绘制出来的P-R曲线的一般是这样的:
关于P-R图形有这么一个直观的认识:若一个模型的曲线把另外一个模型的曲线包住,那么这个模型的性能要由于另外一个模型。
$F1$值和$F_{\beta}$值
单独使用precision和recall的话,那么容易出现一个问题,那就是在有的时候precision和recall这两个值都很高。这个时候可以使用其它的标准,比如上图当中的平衡点,即曲线和y=x曲线的交点。
还可以使用F1值来进行度量:$F1 = \frac{2\times P \times R}{P+R}$
$F_{\beta}$可以选择我们对于precison的值和recall值的权重$$F_{\beta}=\frac{1+{\beta}^2 \times P \times R}{({\beta}^2\times P)+R}$$
当$\beta$的值为1的时候,为$F_{\beta}$变为了$F1$。表示precision和recall的权重是一样的。 当$\bate$的值大于1的时候,recall有更大的影响,$\beta$小于1的时候,precision的值有更大的影响。
ROC和AUC
在混淆矩阵当中还可以定义出来两个变量:
TPR(True Positive Rate)真正例率 模型正确预测的正样本率 $TPR=\frac{TP}{TP+FN}$ 其实和recall是一样的
FPR (False Positive Rate)假正例率 模型错误预测的负样本率 $FPR =\frac{FP}{FP+TN}$
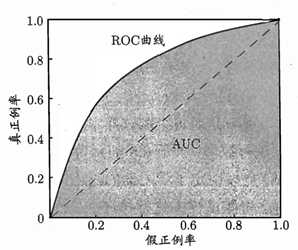
我们以这两个指标来绘制ROC曲线,ROC(Receiver Operating Characteristic) 受试者工作特征曲线。同样,我们的自变量应该是我们的阈值,每得到一个阈值,就有一个TPR和一个FPR与之对应。 当阈值很高的时候,大部分都预测为反例,此时,TPR和FPR都很低。当阈值很高的时候,大部分都预测为正例,此时TPR和FPR都很高。ROC曲线绘制出来的效果如下。
可以看出ROC曲线和P-R曲线 都是以阈值为自变量,使用不同的指标来绘制出来图形。
对于ROC曲线来说,下面的面积是AUC(Area Under Roc Curve),面积越大,模型的性能越好。
为什么要用ROC和AUC哪? 根据这个博客,可以看到当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。
总结一下: 回归问题的性能度量可以使用均方误差,分类问题的性能度量可以使用 accuracy、precision、recall、F1值、$F\beta$值、ROC和AUC。
参考 周志华 《机器学习》 2.3 性能度量