整理自其他优秀博文及自己理解。
目录
- 无约束优化
- 等式约束
- 不等式约束(KKT条件)
1、无约束优化
无约束优化问题即高数下册中的 “多元函数的极值" 部分。
驻点:所有偏导数皆为0的点;
极值点:在邻域内最大或最小的点;
最值点:在定义域内最大或最小的点;
关系:
驻点不一定是极值点,极值点一定是驻点;
极值点不一定是最值点,最值点一定是极值点;
求解最值:
求出所有的极值点,将所有的极值点带入函数中,最大或最小的那个就是最值点。
2、等式约束
等式约束问题即高数下册中的 “条件极值 拉格朗日乘数法” 部分。
对于$z=f(x,y)$在$\varphi(x,y)=0$的条件下的最值问题:
构造拉格朗日函数:$L(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)$;
对拉格朗日函数求解,得到的即为在条件$\varphi(x,y)=0$下,$z=f(x,y)$所有可能的极值点。再利用问题本身的其他约束条件(如果有的话)筛选极值点,比较之后求得最值点。
直观的解释:目标函数和约束函数在最优解处的法线共线,即$\bigtriangledown f(x,y)=\lambda\bigtriangledown g(x,y)$
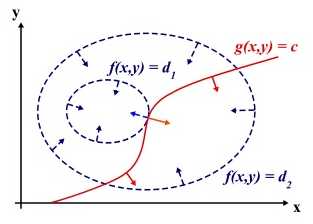
具体证明请查阅高数课本。
3、不等式约束
当约束是不等式的时候,可以在不等式约束中加入松弛变量,使其变为等式约束问题,再进行一些分析。
最后$x^*$是极值点的必要条件(KKT条件)为:
$f(x)=\left\{
\begin{aligned}
\bigtriangledown f(x) & = & \lambda \bigtriangledown c_i(x) \\
\lambda_ic_i(x) & = & 0\\
\lambda_i & \geq & 0
\end{aligned}
\right.$
不等式约束可以直接利用KKT条件求出可能的极值点。
具体推导和证明可参见:https://zhuanlan.zhihu.com/p/26514613
他们之间的关系:(此图来自知乎上链接,入侵可删)
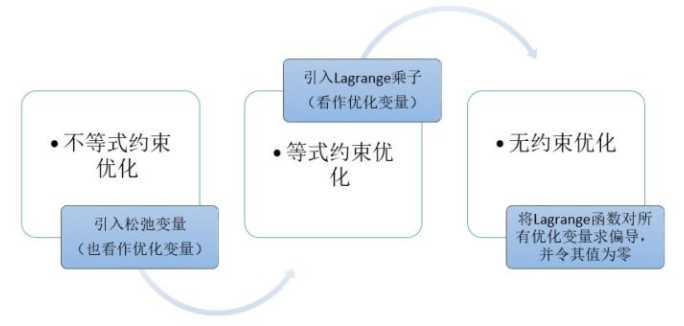
至此,梳理完毕。
