二叉树前驱后继概念及删除操作

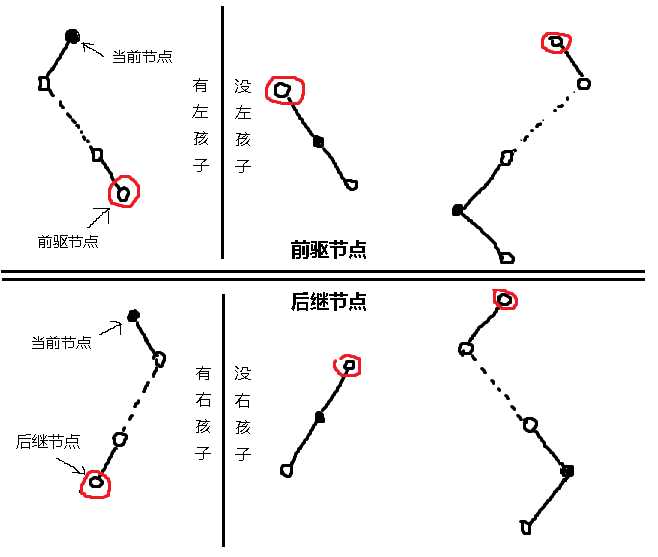
前驱和后继(中序遍历)

节点的前驱：是该节点的左子树中的最大节点。
节点的后继：是该节点的右子树中的最小节点。

理解图：

查找前驱节点的代码

/* 
 * 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
 */
public BSTNode<T> predecessor(BSTNode<T> x) {
    // 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
    if (x.left != null)
        return maximum(x.left);

    // 如果x没有左孩子。则x有以下两种可能：
    //  x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
    //  x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
    BSTNode<T> y = x.parent;
    while ((y!=null) && (x==y.left)) {
        x = y;
        y = y.parent;
    }

    return y;
}

查找后继节点的代码

/* 
 * 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
 */
public BSTNode<T> successor(BSTNode<T> x) {
    // 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
    if (x.right != null)
        return minimum(x.right);

    // 如果x没有右孩子。则x有以下两种可能：
    //  x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
    //  x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
    BSTNode<T> y = x.parent;
    while ((y!=null) && (x==y.right)) {
        x = y;
        y = y.parent;
    }

    return y;
}

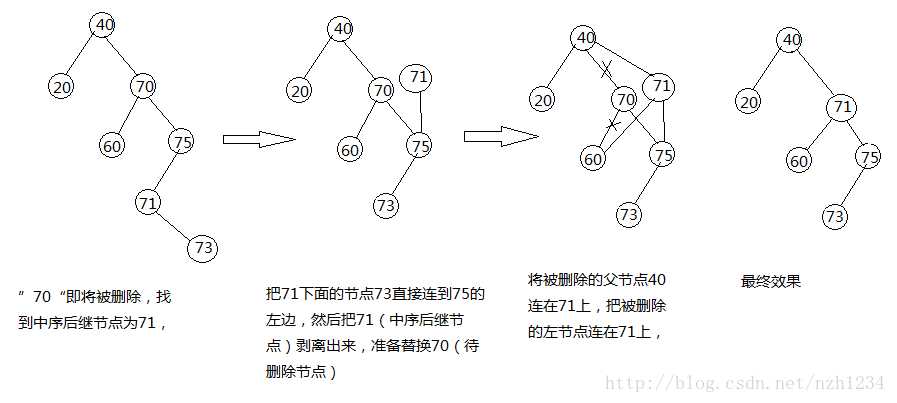
删除

理解图：

代码：

private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z) {
    BSTNode<T> x=null;
    BSTNode<T> y=null;
    /*
    * z: 要删除的节点
    * y: 要代替z的节点
    * x: y的孩子节点。x需替代y的位置。
    *
    * */
    if ((z.left == null) || (z.right == null) )//只有一个孩子或没孩子。
        y = z;
    else//两个孩子，寻找后继
        y = successor(z);
    //选择y下需要上调的孩子--x
    if (y.left != null)
        x = y.left;
    else
        x = y.right;
    //x代替y的位置
    if (x != null)
        x.parent = y.parent;

    if (y.parent == null)
        bst.mRoot = x;
    else if (y == y.parent.left)//是左孩子，则x放左边
        y.parent.left = x;
    else
        y.parent.right = x;

    if (y != z)//如果不是孩子直接替换的情况，要把后继节点值赋给z
        z.key = y.key;

    return y;
}

引用：

　　图2：https://blog.csdn.net/nzh1234/article/details/31076401

　　代码：http://www.cnblogs.com/skywang12345/p/3576452.html