内容:线性回归;逻辑回归,应用场景。
有监督学习,根据学习样本{x->y},学习一个映射f:X->Y(线性相关),输出预测结果y_i。最简单的例子:y=ax+b
重要组成:训练数据集 training set, 学习算法 learning algorithm, 损失函数 loss function.
训练数据集:x-->y的对应数据
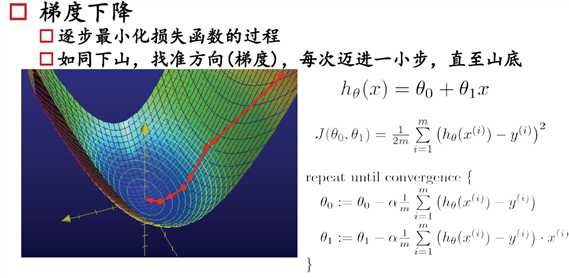
损失函数cost: 权衡训练到的x-y的映射的好坏,最小化这个损失函数。 比较常见的最小二乘法,一般为凸函数
学习算法:梯度下降,逐步最小化损失函数,朝着斜率为负的方向迈进。关键知识点:学习率,终止条件,欠/过拟和,正则化
过拟合:特征过多,对源数据拟合的很好但是丧失了一般性,对预测样本预测效果差
欠拟合:模型没有很好地捕捉到数据特征,不能够很好地拟合数据 。
正则化:类似于模型参数与误差的平方和最小(L2).
例,拟合一个y=ax+b.
取X_i=[x1,x2]^T,$$\theta=[a,b], y_i=\theta*X$$
 ,
,
python代码实现:
##梯度下降的过程
import numpy as np
def gradientDesc(x,y, theta=np.zeros((2,1)),alpha=.01,iterations=1000):
m=y.size
J=[]
for numbers in range(iterations):
a = theta[0][0] - alpha * (1 / m) * sum((x.dot(theta).flatten() - y.flatten() ) * x[:, 0])
b = theta[1][0] - alpha * (1 / m) * sum((x.dot(theta).flatten() - y.flatten() ) * x[:, 1])
theta[0][0],theta[1][0] = a,b
J.append(cost(x,y,theta))
if numbers%100==0:print("第%d步:%.3f,%.3f"%(numbers+100,theta[0][0],theta[1][0]))
return theta
def cost(x,y,theta=np.zeros((2,1))):
m=len(x)
J = 1 / (2 * m) * sum((x.dot(theta).flatten() - y) ** 2)
return J
##测试
x=np.array([[1,2],[2,1],[3,1],[4.1,1]])
y=np.array([[1],[2],[3],[4.1]])
theta = gradientDesc(x,y)
二、逻辑回归
逻辑回归一般解决分类问题,离散点,回归+阈值(sigmoid),损失函数--》判定边界。多分类可以设计多个分类器。
梯度:
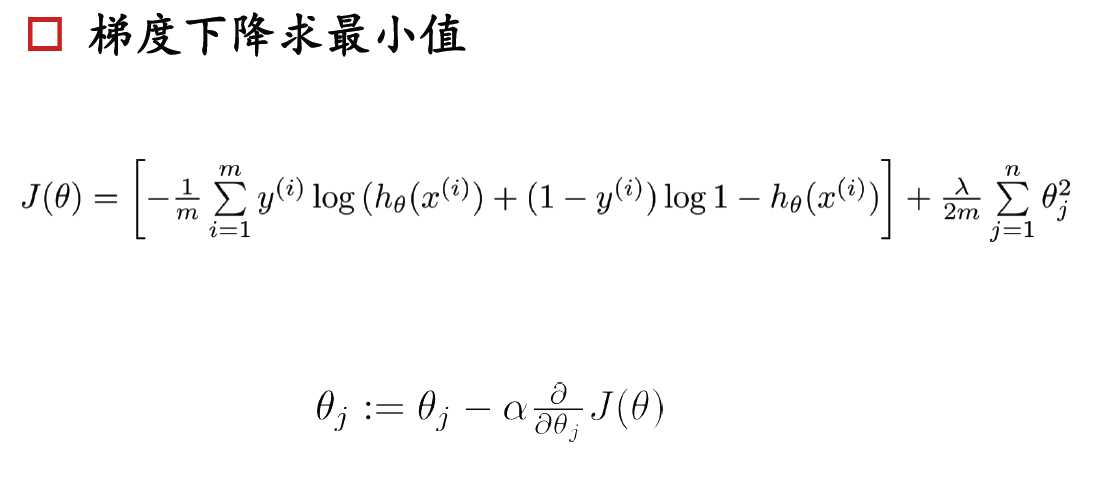
基本函数:
#### 带正则化项的损失函数
#### $$ J(\theta) = \frac{1}{m}\sum_{i=1}^{m}\big[-y^{(i)}\, log\,( h_\theta\,(x^{(i)}))-(1-y^{(i)})\,log\,(1-h_\theta(x^{(i)}))\big] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_{j}^{2}$$
#### 向量化的损失函数
#### $$ J(\theta) = \frac{1}{m}\big((\,log\,(g(X\theta))^Ty+(\,log\,(1-g(X\theta))^T(1-y)\big) + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_{j}^{2}$$
#### 偏导(梯度)
#### $$ \frac{\delta J(\theta)}{\delta\theta_{j}} = \frac{1}{m}\sum_{i=1}^{m} ( h_\theta (x^{(i)})-y^{(i)})x^{(i)}_{j} + \frac{\lambda}{m}\theta_{j}$$
#### 向量化
#### $$ \frac{\delta J(\theta)}{\delta\theta_{j}} = \frac{1}{m} X^T(g(X\theta)-y) + \frac{\lambda}{m}\theta_{j}$$
##### $$\text{Note: 要注意的是参数 } \theta_{0} \text{ 是不需要正则化的}$$
##定义sigmoid函数 def sigmoid(z): return(1 / (1 + np.exp(-z))) # 定义损失函数
def costFunctionReg(theta, reg, *args):
m = y.size
h = sigmoid(XX.dot(theta))
J = -1 * (1 / m) * (np.log(h).T.dot(y) + np.log(1 - h).T.dot(1 - y)) + (reg / (2 * m)) * np.sum(
np.square(theta[1:]))
if np.isnan(J[0]):
return (np.inf)
return (J[0])
def gradientReg(theta, reg, *args):
m = y.size
h = sigmoid(XX.dot(theta.reshape(-1, 1)))
grad = (1 / m) * XX.T.dot(h - y) + (reg / m) * np.r_[[[0]], theta[1:].reshape(-1, 1)]
return (grad.flatten())
