在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;
在理解补码的之前,得先了解另外一个概念:补数;
表示n位的计算机计量范围是0~2^(n)-1,模=2^(n)。
我们以以四位二进制来说明问题:
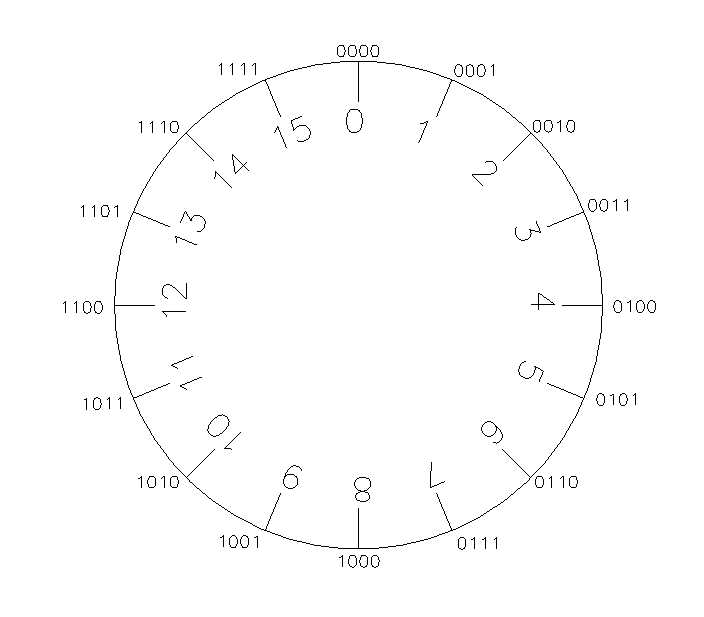
上图中外圈为四位二进制码,内圈为二进制码对应的无符号整数的值。在上图所示的计量系统中,计量的范围为0~15,模为16,所以1和15,2和14,7和9互为补数。所以在上面的计量系统中:
x - 1 = x + (-1) +16 = x +15
x - 2 = x + (-2) +16 = x +14
......
x - 7 = x + (-7) +16 = x + 9
x - 8 = x + (-8) +16 = x + 8
x - 9 = x + (-9) +16 = x + 7
x - 10 = x + (-10) +16 = x +6
......
x - 15 = x + (-15) +16 = x + 1
x - 8 = x + (-8) +16 = x + 8
x - 9 = x + (-9) +16 = x + 7
x - 10 = x + (-10) +16 = x +6
......
x - 15 = x + (-15) +16 = x + 1
可以看出,在上述系统中减去一个正整数m等于加上m的补数!所以在上述计量系统中,在进行加法操作时我们可以用15代替-1,用14代替-2,...,用8代替-8而不影响结果的正确性。而计算机中的减、乘、除操作都会转换成加法操作。所以用15(1111)表示-1等等这些都能保证结果不受影响。所以我们完善一下上面的图,结果如下:
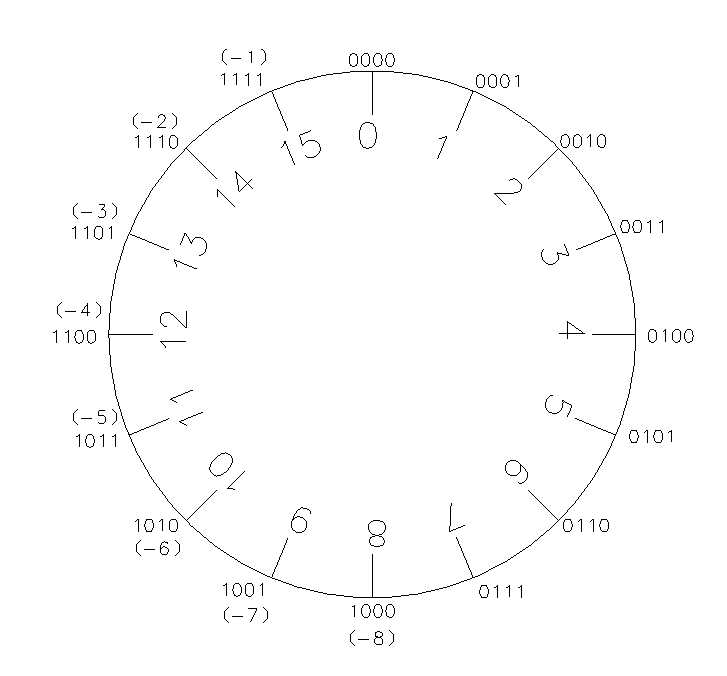
左半圆上二级制码旁边括号中就是它可以代替的负数,负数对应的二进制码就是它的补码;所以说负数求补码就是求对应的正数的补数的过程:负数的绝对值按位求反再加1;
这里没有考虑溢出的问题!
