problem1 link
对于每个质因子$p$,枚举其出现的最少次数以及最多次数分别在哪个数字中.
problem2 link
分数规划.题目是求$\frac{3600K+\sum_{i=0}^{K-1}a_{c_{i}}p_{c_{i}}}{\sum_{i=0}^{K-1}a_{c_{i}}}*totalWork$.其中$c_{i}$是选出的第$i$个元素.二分$\frac{3600K+\sum_{i=0}^{K-1}a_{c_{i}}p_{c_{i}}}{\sum_{i=0}^{K-1}a_{c_{i}}}$的值,然后选择$a_{i}(result-p_{i})$中最大的$K$个,看是否大于$3600K$.
problem3 link
到达最下面一行或者最右边一列时,只能朝一个方向走.设$f(i)$表示从(0,0)走到(n-1,i)的方案数(最后一步是从(n-2,i)到(n-1,i)),以及$g(i)$表示从$(0,0)$走到(i,m-1)的方案数(最后一步从$(i,m-2)$到(i,m-1)).这两个是类似的.考虑$f(i)$.
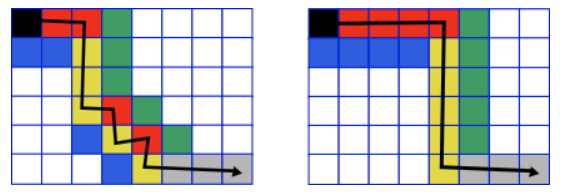
如下面的图示($n=6,m=8,i=4$)的两种走法,可以发现,横向走了红色的四个以及纵向走了黄色的5个,且最后一步到达$(n-1,i)$是黄色.
每次横向走时,需要对应的红色大于等于对应的蓝色;纵向走时,需要对应的黄色大于对应的绿色.
从(0,0)走到$(n-1,i)$一共走了$(i+n-1)$个格子,其中红色可以选择在这个序列的前$(i+n-2)$个中出现(最后一个一定是黄色).
code for problem1
#include <vector>
using namespace std;
class FoxAndGCDLCM {
using Type = std::pair<long long, int>;
public:
long long get(long long G, long long L) {
if (G > L) {
return -1;
}
std::vector<Type> a = split(G);
std::vector<Type> b = split(L);
merge(a, b);
for (size_t i = 0; i < a.size(); ++i) {
if (a[i] > b[i]) {
return -1;
}
}
min_value = -1;
dfs(0, a, b, 1ll, 1ll);
return min_value;
}
private:
void dfs(int dep, const std::vector<Type> &a, std::vector<Type> &b,
long long x, long long y) {
if(dep == a.size()) {
if (min_value == -1 || min_value > x + y) {
min_value = x + y;
}
return;
}
const long long p = pow(a[dep].first, a[dep].second);
const long long q = pow(b[dep].first, b[dep].second);
dfs(dep + 1, a, b, x * p, y * q);
dfs(dep + 1, a, b, x * q, y * p);
}
std::vector<Type> split(long long x) {
std::vector<Type> result;
for (long long t = 2; t * t <= x; ++t) {
if (x % t == 0) {
int num = 0;
while (x % t == 0) {
x /= t;
++num;
}
result.emplace_back(t, num);
}
}
if (x > 1) {
result.emplace_back(x, 1);
}
return result;
}
void merge(std::vector<Type> &a, std::vector<Type> &b) {
std::vector<Type> ra, rb;
std::size_t i = 0, j = 0;
while (i < a.size() || j < b.size()) {
if (i == a.size() || (j < b.size() && a[i].first > b[j].first)) {
rb.emplace_back(b[j]);
ra.emplace_back(b[j].first, 0);
++j;
} else if (j == b.size() || (i < a.size() && a[i].first < b[j].first)) {
ra.emplace_back(a[i]);
rb.emplace_back(a[i].first, 0);
++i;
} else {
ra.emplace_back(a[i++]);
rb.emplace_back(b[j++]);
}
}
a = ra;
b = rb;
}
long long pow(long long a, int b) {
long long result = 1;
while (b > 0) {
if (b & 1) {
result *= a;
}
a *= a;
b >>= 1;
}
return result;
}
long long min_value;
};
code for problem2
#include <algorithm>
#include <iostream>
class FoxAndBusiness {
public:
double minimumCost(int K, int totalWork, std::vector<int> a,
std::vector<int> p) {
const size_t n = a.size();
double low = 0.0, high = 1e10;
for (int i = 0; i < 200; ++i) {
double mid = (low + high) * 0.5;
std::vector<double> det(n);
for (size_t j = 0; j < n; ++j) {
det[j] = a[j] * (mid - p[j]);
}
std::sort(det.rbegin(), det.rend());
double sum = 0;
for (int j = 0; j < K; ++j) {
sum += det[j];
}
if (sum >= K * 3600) {
high = mid;
} else {
low = mid;
}
}
return low * totalWork;
}
};
code for problem3
#include <algorithm>
#include <iostream>
using namespace std;
class FoxAndGreed {
private:
static const int MOD = 10007;
static void Add(int &x, int y) {
x += y;
if (x >= MOD) {
x -= MOD;
}
}
public:
int count(int H, int W, int S) {
Init(H, W, S);
if (std::min(H, W) == 1) {
return f3[W * H - 1][S];
}
int result = 0;
for (int i = 0; i <= W - 2; ++i) {
int h = i;
int v = H - 1;
int r = W - i - 1;
Add(result, Binomial(h + v - 1, h) *
Pow(S + 1, W * H - 1 - h * 2 - v * 2 - r) % MOD *
Compute(h, v, r, S) % MOD);
}
for (int i = 0; i <= H - 2; ++i) {
int h = W - 1;
int v = i;
int r = H - i - 1;
Add(result, Binomial(h + v - 1, v) *
Pow(S + 1, W * H - 1 - h * 2 - v * 2 - r) % MOD *
Compute(h, v, r, S) % MOD);
}
return result;
}
private:
int Compute(const int h, const int v, int r, const int S) {
int result = 0;
for (int x = 0; x <= S; ++x) {
for (int y = 0; y + x <= S; ++y) {
int z = S - x - y;
Add(result, f1[h][x] * f2[v][y] % MOD * f3[r][z] % MOD);
}
}
return result;
}
void Init(const int H, const int W, const int S) {
auto SetSize = [H, W, S](std::vector<std::vector<int>> &f) {
f.resize(H + W + 2);
for (size_t i = 0; i < f.size(); ++i) {
f[i].resize(S + 1);
}
};
SetSize(f1);
SetSize(f2);
SetSize(f3);
f1[0][0] = f2[0][0] = f3[0][0] = 1;
for (int i = 1; i <= H + W + 1; ++i) {
for (int j = 0; j <= S; ++j) {
f1[i][j] = f2[i][j] = f3[i][j] = 0;
for (int x = 0; x <= j; ++x) {
Add(f1[i][j], f1[i - 1][j - x] * (x + 1) % MOD);
Add(f2[i][j], f2[i - 1][j - x] * x % MOD);
Add(f3[i][j], f3[i - 1][j - x]);
}
}
}
fact.resize(H + W + 2);
invFact.resize(H + W + 2);
fact[0] = invFact[0] = 1;
for (size_t i = 1; i < fact.size(); ++i) {
fact[i] = fact[i - 1] * i % MOD;
invFact[i] = Pow(fact[i], MOD - 2);
}
}
int Binomial(int n, int m) {
return fact[n] * invFact[m] % MOD * invFact[n - m] % MOD;
}
static int Pow(int a, int b) {
int r = 1;
while (b > 0) {
if (b & 1) {
r = r * a % MOD;
}
a = a * a % MOD;
b >>= 1;
}
return r;
}
std::vector<std::vector<int>> f1, f2, f3;
std::vector<int> fact, invFact;
};
