[Bzoj4570][Scoi2016]妖怪（右上凸包）

4570: [Scoi2016]妖怪

Time Limit: 10 Sec Memory Limit: 64 MB
Submit: 1110 Solved: 336
[Submit][Status][Discuss]

Description

邱老师是妖怪爱好者，他有n只妖怪，每只妖怪有攻击力atk和防御力dnf两种属性。邱老师立志成为妖怪大师，于

是他从真新镇出发，踏上未知的旅途，见识不同的风景。环境对妖怪的战斗力有很大影响，在某种环境中，妖怪可

以降低自己k×a点攻击力，提升k×b点防御力或者，提升自己k×a点攻击力，降低k×b点防御力，a，b属于正实数

，k为任意实数，但是atk和dnf必须始终非负。妖怪在环境(a,b)中的战斗力为妖怪在该种环境中能达到的最大攻击

力和最大防御力之和。strength(a,b)=max(atk(a,b))+max(dnf(a,b))环境由a，b两个参数定义，a，b的含义见前

文描述。比如当前环境a=3，b=2，那么攻击力为6，防御力为2的妖怪，能达到的最大攻击力为9，最大防御力为6。

所以该妖怪在a=3，b=2的环境下战斗力为15。因此，在不同的环境，战斗力最强的妖怪可能发生变化。作为一名优

秀的妖怪训练师，邱老师想发掘每一只妖怪的最大潜力，他想知道在最为不利的情况下，他的n只妖怪能够达到的

最强战斗力值，即存在一组正实数(a,b)使得n只妖怪在该环境下最强战斗力最低。

Input

第一行一个n，表示有n只妖怪。接下来n行，每行两个整数atk和dnf，表示妖怪的攻击力和防御力。

1≤n≤10^6, 0＜atk,dnf≤10^8

Output

输出在最不利情况下最强妖怪的战斗力值，保留4位小数。

Sample Input

Sample Output

8.0000

分析

虽然是看了别人的博客才写起的，但也要写博客加深印象。

设atk为x，dnf为y。那么每个妖怪能看成平面上的一个点（x，y）

设最强战斗力为L

合并一下

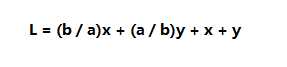
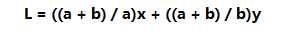
发现是L是一条斜率-b/a的直线。

如果已知直线L，在它下最强的妖怪是谁呢？

那么画图来试试，一大堆小点点是一个妖怪，然后右上角是维护的右上凸包

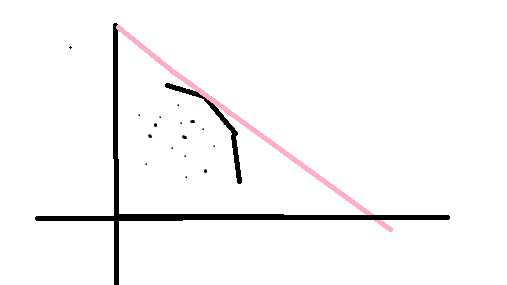
技术分享图片

发现粉色直线与右上凸包的切点是在它下的最强妖怪

为什么是右上凸包与它切点最优，因为我们答案是横纵截距之和，我们把直线往下平移发现横纵截距都在减小，肯定不会比切点的战斗力小

已知右上凸包怎么对右上凸包每个点求出一个最优的斜率k使它为切点？

可以得出结论：斜率一定是大于它与上一个点连线的斜率，小于它与下一个点连线的斜率

设右上凸包每一个点与下一个点连线斜率为ki

那么斜率k就在这个范围内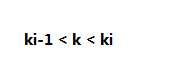技术分享图片，我们要在这个范围内求一个点使答案最小。

当我们已知点（x，y）求L时，x，y变成了常数，又斜率k为-b/a

那么答案可以表示为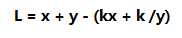技术分享图片

发现是个双钩函数，在k = -（x/y）^½时取最小。

因为是双钩函数不满足单调，我就去三分了，然后华丽丽T了。

其实我们可以判断一下双钩函数顶点是否在合法范围内，是的话取最小值

不是的话肯定是关于双钩函数的一边，则具有单调性。

那么此时我就想到二分了。。。然后完美地t了

正解：

合法范围ki-1和ki一定是双钩函数定义域的端点。每个点可以用ki算一次答案，如果顶点在定义域内还可以算一次答案

AC代码：

# include <iostream>
# include <cstdio>
# include <cstring>
# include <cmath>
# include <algorithm>
using namespace std;
const int N = 1e6 + 12;
const double eps = 1e-6;
const double inf = 0x3f3f3f3f;
struct Point{
    double x,y;
    Point(){}
    Point(double a,double b) : x(a),y(b){}
    void read(){scanf("%lf %lf",&x,&y);}
    double com(){return x + y + 2 * sqrt(x * y);}
    bool operator <(const Point & other)const{return x == other.x ? y > other.y : x > other.x;}
}a[N];
int n,ed;double k[N],ans = inf;
Point operator -(Point a,Point b){return Point(a.x - b.x,a.y - b.y);}
double Get(Point a){return a.y / a.x;}
double Cross(Point a,Point b){return a.x * b.y - a.y * b.x;}
int main()
{
  scanf("%d",&n);
  for(int i = 1;i <= n;i++)a[i].read();
  sort(a + 1,a + n + 1);int top = 1;
  for(int i = 2;i <= n;i++)
  {
      while(top > 1 && Cross(a[i] - a[top],a[top] - a[top - 1]) >= 0)top--;
      a[++top] = a[i];
  }
  a[top + 1] = Point(0,0);
  for(int i = 1;i <= top;i++)
  {
      k[i] = Get(a[i + 1] - a[i]);
      ed = i;if(k[i] >= 0)break;
  }
  k[ed] = -eps;k[0] = -inf;
  for(int i = 1;i <= ed;i++)
  {    
      double mk = -sqrt(a[i].y / a[i].x),cg = inf,he;
      if(mk > k[i - 1] && mk < k[i])cg = a[i].com();
      he = a[i].x + a[i].y - a[i].x * k[i] - a[i].y / k[i];
      cg = cg > he ? 
    he : cg;ans = ans > cg ? cg : ans;
  }
  printf("%.4lf\n",ans);
}