一、PTA实验作业

题目一：6-2 线性表元素的区间删除

设计思路

定义i控制循环，count进行控制是否要删除的数字
if 最大值小于最小值，返回L
for i=0 to   i<=L->Last 
       if  L->data在所要删除的区间范围内
                    count++
       else
                L->Data[i-count]=L->Data[i];//进行删除数字
                                         end
   L的长度等于之前的长度减去count
     返回L；

代码截图

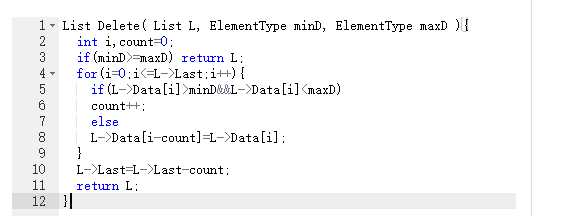
PTA提交列表说明。

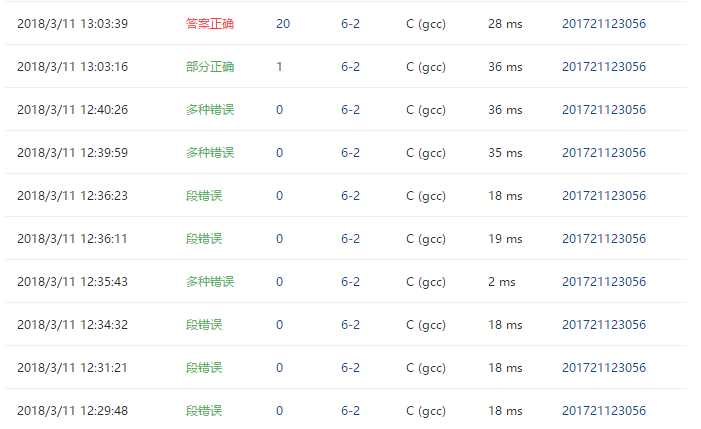
• 主要是时间复杂度太大了，之前用了两个循环，后面改成一个循环就可以了。

题目2：6-2 jmu-ds-单链表逆置

设计思路

输入函数：
       定义链表；类型 s，r；
       定义i来控制循环，m用来输入数据；
         给L创建头结点； 
           r始终指向尾节点，开始时指向头结点；
for  i=0 to   n-1  //循环建立数据节点
    创建数据节点s；
      将s插入r之后；//尾插法
                   end;
   ’尾节点next域置为NULL；

输出函数：
    定义p指向L的next域置；
       if  p为空
           输出NULL；
      else
          输出第一个数据，前面无空格
           p指向p的next域置
         while（p）
             先输出一个空格，在输出数据
                 p指向p的next域置
                                      end；

倒置函数：
      定义 p,q;
        p指向L的next，L的next置为空；
          while(p)   //头插法
                     q指向p的next域置
                    p的next域置等于L的next域置  
                    L的next域置等于p；
                    p=q；
                                     end；

3.代码截图

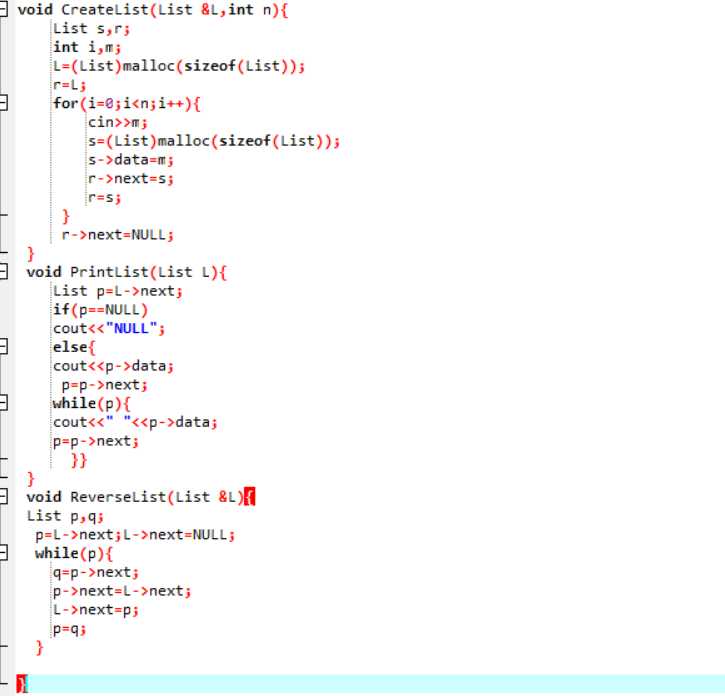
4.PTA提交列表说明。

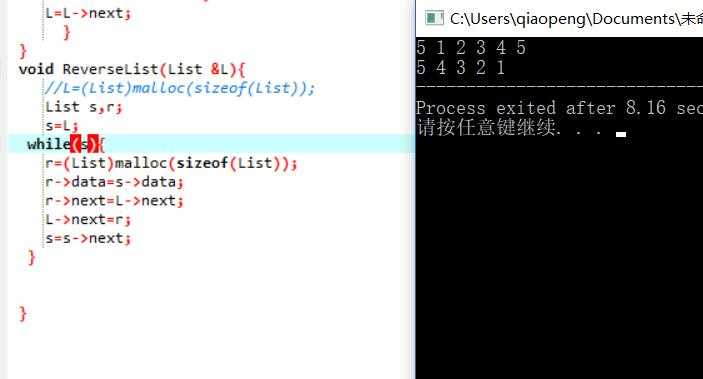
• 最后面那个链表倒置一直运行错误，错误如上图，一开始效仿尾插法也建立数据节点，一直运行错误，有时候结果出来了也是提示运行错误，后来搞不懂去请教同学，发现其实不用创建数据节点，然后我把数据节点去掉，再运用头插法就行了。

  题目3:7-1 两个有序链表序列的合并

  设计思路

  输入函数void CreateListR(List &s,ElemType a[],int n);
  创建头结点L,List r,p;
  r始终指向尾节点，开始时指向头结点
      for i=0  to    i<n
          创建数据节点p
           将p插入r之后
                           end；
   尾节点next的域置为NULL；

  输出函数void DispList(List &s)；
   定义p指向s的next域置；
     if  p为空
         输出NULL；
    else
        输出第一个数据，前面无空格
         p指向p的next域置
       while（p）
           先输出一个空格，在输出数据
               p指向p的next域置
                                    end；
              换行；                        end；

  合并函数void sort(List s1,List s2,List &s3)；
   List pa=s1->next, pb=s2->next,r,p;
    创建s3的头结点
      r始终指向s3的尾节点
  whilewhile(pa!=NULL&&pb!=NULL)
     if pa->data的数据小于pa->data的数据
         复制pb节点
           采用尾插法将p插入到s3中
    else  
          复制pa节点
            采用尾插法将p插入到s3中   end；
      while（pa不为空）
           复制pa节点
            采用尾插法将p插入到s3中   end；
       while（pb不为空）
           复制pb节点
            采用尾插法将p插入到s3中   end；
       r尾节点next的域置为NULL；

  3.代码截图

  
  
  

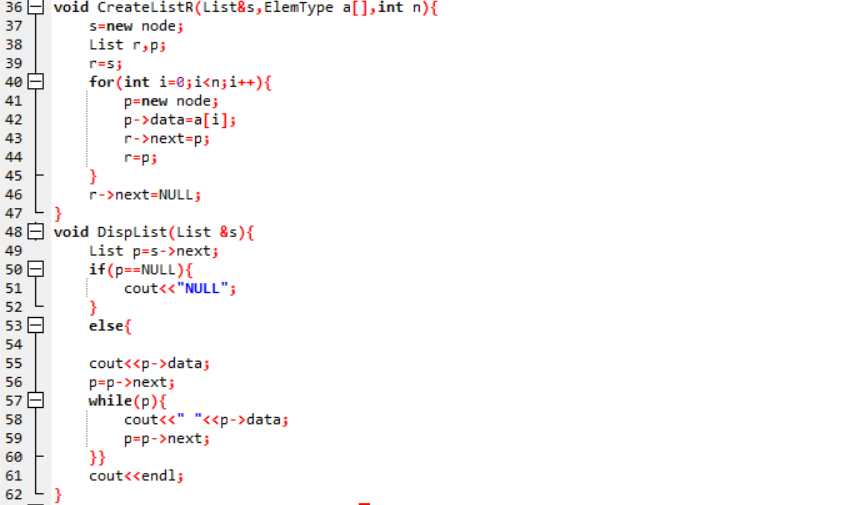
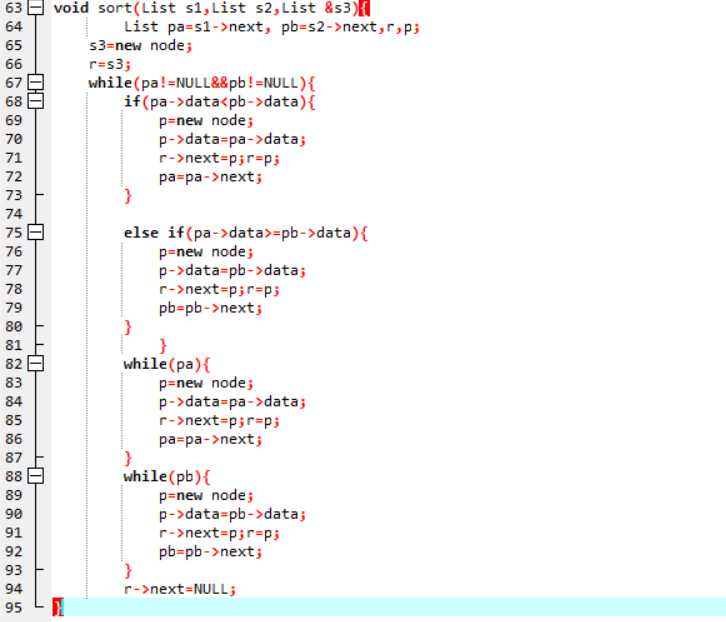
  4.PTA提交列表说明。

  
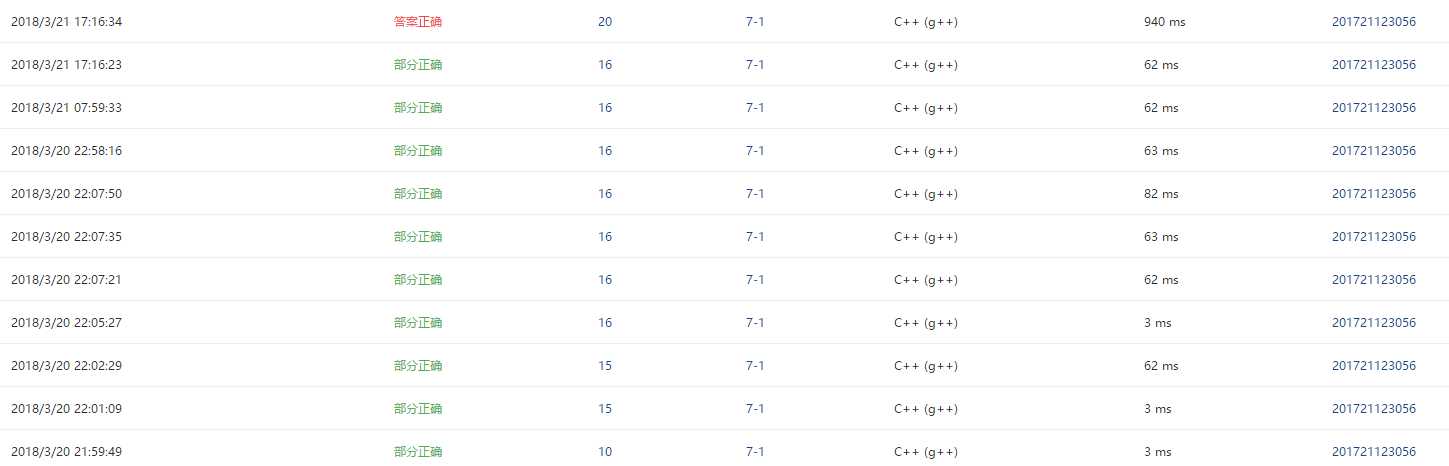
  这题主要是大规模输入出现段错误，一开始不知道怎么改，然后随便把数组弄到1000001，一提交就对了。但是这样在DVC那边运行不了，具体如何解决现在还不是很了解。除了把数组调到1000001

  二、截图本周题目集的PTA最后排名

  1.顺序表PTA排名

  

  2.链表PTA排名

  

  3.我的总分：

  85+150=235

  三、本周学习总结

  1.谈谈你本周数据结构学习时间是如何安排，对自己安排满意么，若不满意，打算做什么改变？

• 没课的时候就抽时间来完成作业还有自习的时候来学习
• 编程也是空闲的时候来完成PTA，分时间来完成，能写一题是一题

• 不懂的话先翻书看书里有没有相应内容，没有自己再思考，想不出来就缓一下去问同学，同学也不懂的话就去网上查思路。

  2.谈谈你对线性表的认识？

• 链表为动态存储结构，可以随时申请或归还存储空间，且插入或删除结点时，只要修改链接的指针，不需移动数据结点，时间复杂度为O(1)，它的缺点是不能随机访问数据节点，需要遍历链表，时间复杂度为O(n)。

• 本次7-2用链表来完成的话后面的指数排序我觉得有点难，写了有点久，最会放弃了，改用数组来完成，所以链表有好处也有坏处。

  3.代码Git提交记录截图

  四.代码互评

  #include <stdio.h>
  #include <stdlib.h>
  typedef struct _RingNode
  {
   int pos;
   struct _RingNode *next;
  }RingNode, *RingNodePtr;
  void CreateRing(RingNodePtr pHead, int count)
  {
   RingNodePtr pCurr = NULL, pPrev = NULL;
   int i = 1;
   pPrev = pHead;
   while(--count > 0)
    {
        pCurr = (RingNodePtr)malloc(sizeof(RingNode));
        i++;
        pCurr->pos = i;
        pPrev->next = pCurr;
        pPrev = pCurr;
    }
    pCurr->next = pHead;
    }
  void KickFromRing(RingNodePtr pHead, int m)
  {
   RingNodePtr pCurr, pPrev;
   int i = 1;    // 计数
   pCurr = pPrev = pHead;
   while(pCurr != NULL)
   {
       if (i == m)
       {
            pPrev->next = pCurr->next;
            free(pCurr);
            pCurr = pPrev->next;
            i = 1;
       }
        pPrev = pCurr;
        pCurr = pCurr->next;
        if (pPrev == pCurr)
        {
            printf("%d\n", pCurr->pos);
            free(pCurr);
            break;
        }
        i++;
    }
  }
  int main()
  {
   int n, m;
   RingNodePtr pHead = NULL;
   scanf("%d %d", &n,&m);
    pHead = (RingNodePtr)malloc(sizeof(RingNode));
    pHead->pos = 1;
    pHead->next = NULL;
    CreateRing(pHead, n);
   KickFromRing(pHead, m);
   return 0;
  }

• 这代码虽然用的是C语言，但这是一个典型的需要用双链表来解决的约瑟夫环问题