Wannafly挑战赛12 D矩阵计数
题意:给一个n x m的01矩阵,其中C个格子是1,其余全是0。求有多少全0的子矩阵。
答案对\(10^9+7\)取模。思路:首先,全0的子矩阵=所有子矩阵-含1的子矩阵, 我们只需要对所有的值为1的格子,求出包含这个点的子矩阵数量\(s_i\)(还要保证不重复计数),那么\(ans = \sum_{i=1}^{C}s_i\)
- 如何求\(s_i\):
首先来看一个例子,如图:
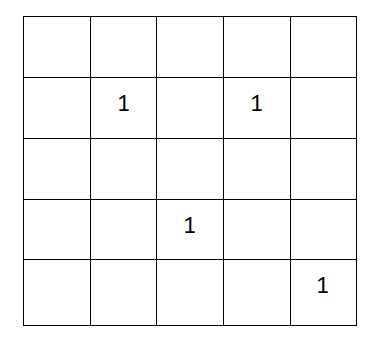
- 对于所有值为1的格子,我们先排序(先按x轴再按y轴排),对于上图中的第一个点(2, 2),先计算包含这个点的所有子矩阵,显然是\((x-1+1)*(y-1+1)*(n-x)*(m-y+1)=2*2*4*4=64\),(x-1+1),(y-1+1),(n-x),(m-y+1)分别代表这个点距上边界,左边界,下边界,右边界的距离;
再看第二个点, 由于要保证不会重复计数,计算\(s_2\)时不能包含第一个点,所以需要计算的部分如下图:
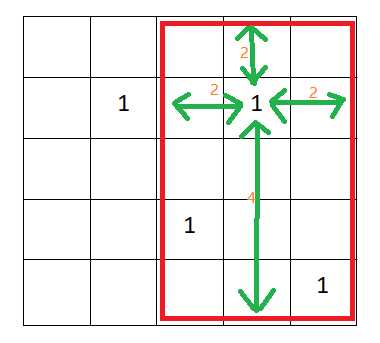
第三个点:
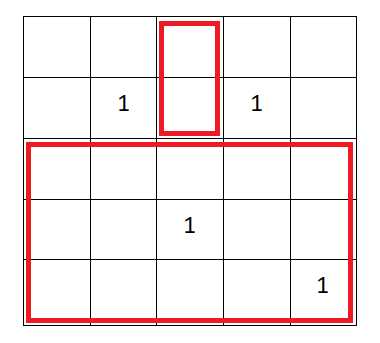
- 总结:对于每个点,我们可以找到它再每一行可以拓展到的最大左右区间,然后乘以这个区间的高度和这个点到最后一行的距离,然后求和即是我们要求的\(s_i\)。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5005;
const ll mod = 1e9+7;
int n, m, c;
struct P{
int x, y;
P() {}
P(int x, int y): x(x), y(y) {}
bool operator < (const P &t) const {
return x == t.x ? y < t.y : x < t.x;
}
} p[maxn];
int main() {
while(~scanf("%d %d %d", &n, &m, &c)) {
for(int i = 1; i <= c; i++) {
scanf("%d %d", &p[i].x, &p[i].y);
}
sort(p + 1, p + c + 1);
ll ans = 0;
for(int i = 1; i <= c; i++) {
for(int j = i - 1, l = 1, r = m; j >= 0; j--) {
if(p[j+1].x != p[j].x) ans=(ans+(n-p[i].x+1LL)%mod*(r-p[i].y+1)%mod*(p[i].y-l+1)%mod*(p[j+1].x-p[j].x)%mod)%mod;
if(p[j].y < p[i].y) l = max(l, p[j].y+1);
if(p[j].y > p[i].y) r = min(r, p[j].y-1);
}
}
printf("%lld\n", ((n*(n+1LL)/2)%mod*((m*(m+1LL)/2)%mod)%mod-ans+mod) % mod);
}
return 0;
}