选择题目

题目一：最大连续子数组和（最大子段和）

背景:

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。-- 引用自《百度百科》

题目二：下表为某商场每日营业额与应收税率的对照表，请编写一小程序根据该商场每日营业额计算其实际应缴纳税费。

本次作业选择题目一（最大连续子数组和（最大子段和））完成

测试要求

1.请从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、>条件组合覆盖五个覆盖标准中（条件组合覆盖难度较大，鼓励尝试，但请谨慎选择），任选一个标准设计测试用例。
2.请利用自动测试工具对程序进行测试。
3.请将程序运行结果和自动测试分析结果截图附到博客中。

算法分析

根据分治法：
如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和，则a[1:n]的最大子段和有三种情况：

（1） a[1:n]的最大子段和与a[1:n/2]的最大子段和相同
（2） a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同
（3） a[1:n]的最大子段和为a[i]+…+a[j]，并且1<=i<=n/2，n/2+1<=j<=n。

在对于上述分治算法的分析中我们注意到，若记b[j]=max(a[i]+a[i+1]+..+a[j]),其中1<=i<=j,并且1<=j<=n。则所求的最大子段和为max b[j]，1<=j<=n。
由b[j]的定义可易知，当b[j-1]>0时b[j]=b[j-1]+a[j]，否则b[j]=a[j]。故b[j]的动态规划递归式为:

                           b[j]=max(b[j-1]+a[j],a[j])，1<=j<=n。

算法代码：

        b[0]=a[0];max=b[0];
        for(i=1; i<k; i++) {
        if(b[i-1]>0)
            b[i]=b[i-1]+a[i];
        else
            b[i]=a[i];
        if(b[i]>max)
            max=b[i];｝

根据算法画出程序框图如下：

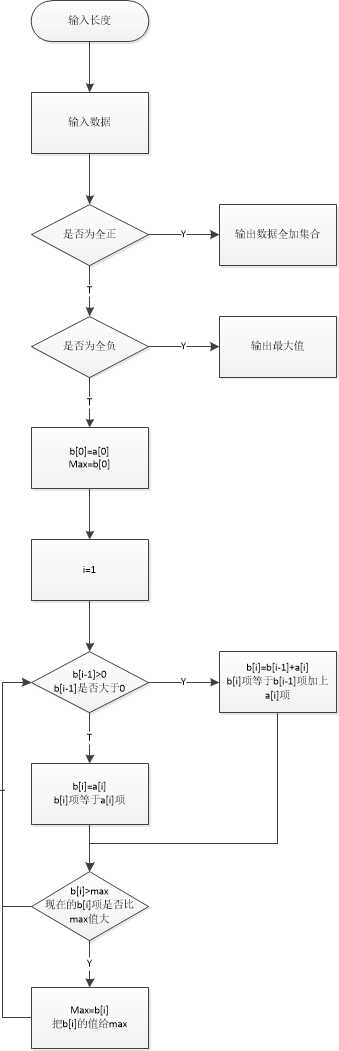
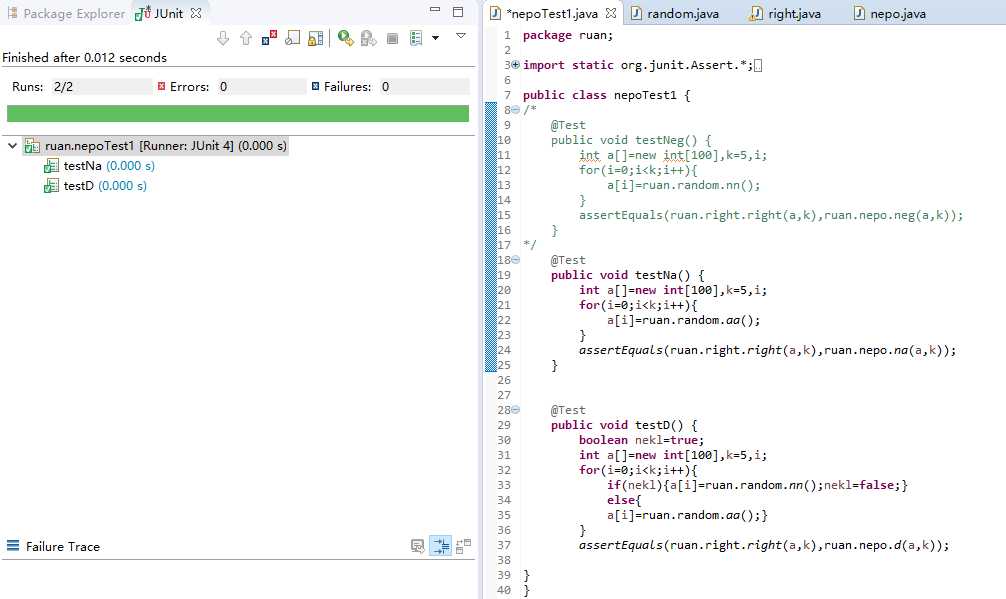
单元测试

本次单元测试采用条件覆盖：

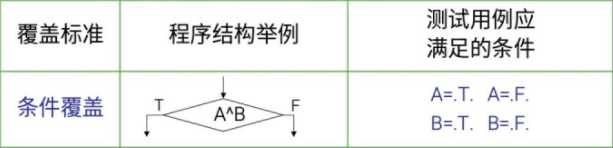
根据设计要求生成出符合单元测试的随机数，将随机数送入绝对正确的函数中计算，再与本程序对比。如单元测试通过，则证明程序正确。
其中，本次单元测试中绝对正确的函数采用至博文：秦川德利齐。
代码如下：

测试结果

最后经过多轮测试，所有样例均通过测试。