一 批标准化 (batch normalization)
部分内容来自:
深度学习Deep Learning(05):Batch Normalization(BN)批标准化
参考论文:http://jmlr.org/proceedings/papers/v37/ioffe15.pdf
- 2015年Google提出的Batch Normalization
- 训练深层的神经网络很复杂,因为训练时每一层输入的分布在变化,导致训练过程中的饱和,称这种现象为:internal covariate shift。
- 需要降低学习率Learning Rate和注意参数的初始化,论文中提出的方法是对于每一个小的训练batch都进行标准化(正态化)
- 允许使用较大的学习率。
- 不必太关心初始化的问题。
- 同时一些例子中不需要使用Dropout方法避免过拟合。
- 此方法在ImageNet classification比赛中获得4.82% top-5的测试错误率。
批标准化通俗来说就是对每一层神经网络进行标准化 (normalize) 处理, 我们知道对输入数据进行标准化能让机器学习有效率地学习,如果把每一层都
看成这种接受输入数据的模式。
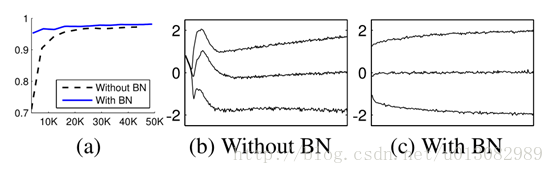
我们先来看看下面的两个动图, 了解下在每层神经网络有无 batch normalization 的区别。
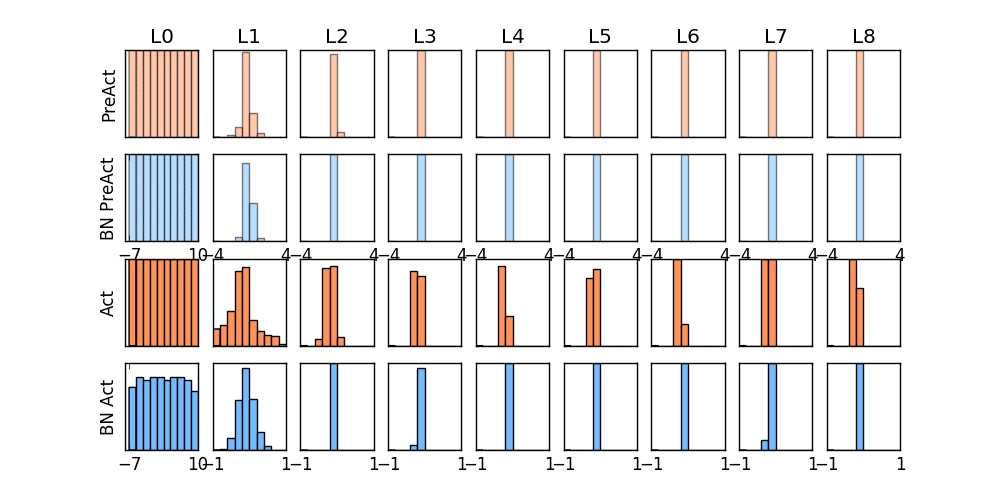
其中PreAct表示加权输出值z,BN PreAct表示经过批标准化之后的输出a。Act表示激活函数输出z,BN Act表示BN PreAct经过激活函数的输出a。
第一幅图片激活函数选择的是ReLU,第二幅图片选择的激活函数是Sigmoid函数。
看第一幅图,我们可以看到在L2层之后,PreAct,以及Act输出基本都为0了,说明神经网络已经不起任何作用了。而经过BN处理后,我们可以看到
神经网络可以正常工作。详细内容参考这里。

BN算法
-
-
如果输入数据是白化的(whitened),网络会更快的收敛
- 白化目的是降低数据的冗余性和特征的相关性,例如通过线性变换使数据为0均值和单位方差
-
并非直接标准化每一层那么简单,如果不考虑归一化的影响,可能会降低梯度下降的影响
- 标准化与某个样本和所有样本都有关系
- 解决上面的问题,我们希望对于任何参数值,都要满足想要的分布;
- 对于反向传播,需要计算:
和
- 这样做的计算代价是非常大的,因为需要计算x的协方差矩阵
- 然后白化操作:
- 上面两种都不行或是不好,进而得到了BN的方法
- 既然白化每一层的输入代价非常大,我们可以进行简化
- 简化1
- 标准化特征的每一个维度而不是去标准化所有的特征,这样就不用求协方差矩阵了
- 例如
d维的输入: - 标准化操作:
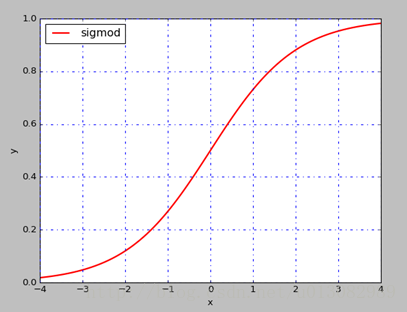
- 需要注意的是标准化操作可能会降低数据的表达能力,例如我们之前提到的Sigmoid函数:
- 标准化之后均值为0,方差为1,数据就会落在近似线性的函数区域内,这样激活函数的意义就不明显
- 所以对于每个 ,对应一对参数:
,然后令:
- 从式子来看就是对标准化的数据进行缩放和平移,不至于使数据落在线性区域内,增加数据的表达能力(式子中如果:
,
,就会使恢复到原来的值了)
- 但是这里还是使用的全部的数据集,但是如果使用随机梯度下降,可以选取一个batch进行训练
-
简化2
- 第二种简化就是使用
mini-batch进行随机梯度下降 - 注意这里使用
mini-batch也是标准化每一个维度上的特征,而不是所有的特征一起,因为若果mini-batch中的数据量小于特征的维度时,会产生
- 第二种简化就是使用
-
奇异协方差矩阵, 对应的行列式的值为0,非满秩
-
- 假设mini-batch 大小为
m的B ,对应的变换操作为:
- 作者给出的批标准化的算法如下:
- 算法中的
ε是一个常量,为了保证数值的稳定性
- 假设mini-batch 大小为
-
反向传播求梯度:
- 因为:
- 所以:
- 因为:
- 所以:
- 因为:
和
- 所以:
- 所以:
- 因为:
- 对于BN变换是可微分的,随着网络的训练,网络层可以持续学到输入的分布。
BN网络的训练和推断
- 按照BN方法,输入数据
x会经过变化得到BN(x),然后可以通过随机梯度下降进行训练,标准化是在mini-batch上所以是非常高效的。 - 但是对于推断我们希望输出只取决于输入,而对于输入只有一个实例数据,无法得到
mini-batch的其他实例,就无法求对应的均值和方差了。 - 可以通过从所有训练实例中获得的统计量来**代替**mini-batch中m个训练实例获得统计量均值和方差
- 我们对每个
mini-batch做标准化,可以对记住每个mini-batch的B,然后得到全局统计量 (这里方差采用的是无偏方差估计)
- 所以推断采用
BN的方式为:
- 作者给出的完整算法:
实验
- 最后给出的实验可以看出使用BN的方式训练精准度很高而且很稳定。