实例:
我们将建立一个逻辑回归模型来预测一个学生是否被大学录取。
假设你是一个大学系的管理员,你想根据两次考试的结果来决定每个申请人的录取机会。
你有以前的申请人的历史数据,你可以用它作为逻辑回归的训练集。
对于每一个培训例子,你有两个考试的申请人的分数和录取决定。
为了做到这一点,我们将建立一个分类模型,根据考试成绩估计入学概率。
data.txt:
34.62365962451697,78.0246928153624,0 30.28671076822607,43.89499752400101,0 35.84740876993872,72.90219802708364,0 60.18259938620976,86.30855209546826,1 79.0327360507101,75.3443764369103,1 45.08327747668339,56.3163717815305,0 61.10666453684766,96.51142588489624,1 75.02474556738889,46.55401354116538,1 76.09878670226257,87.42056971926803,1 84.43281996120035,43.53339331072109,1 95.86155507093572,38.22527805795094,0 75.01365838958247,30.60326323428011,0 82.30705337399482,76.48196330235604,1 69.36458875970939,97.71869196188608,1 39.53833914367223,76.03681085115882,0 53.9710521485623,89.20735013750205,1 69.07014406283025,52.74046973016765,1 67.94685547711617,46.67857410673128,0 70.66150955499435,92.92713789364831,1 76.97878372747498,47.57596364975532,1 67.37202754570876,42.83843832029179,0 89.67677575072079,65.79936592745237,1 50.534788289883,48.85581152764205,0 34.21206097786789,44.20952859866288,0 77.9240914545704,68.9723599933059,1 62.27101367004632,69.95445795447587,1 80.1901807509566,44.82162893218353,1 93.114388797442,38.80067033713209,0 61.83020602312595,50.25610789244621,0 38.78580379679423,64.99568095539578,0 61.379289447425,72.80788731317097,1 85.40451939411645,57.05198397627122,1 52.10797973193984,63.12762376881715,0 52.04540476831827,69.43286012045222,1 40.23689373545111,71.16774802184875,0 54.63510555424817,52.21388588061123,0 33.91550010906887,98.86943574220611,0 64.17698887494485,80.90806058670817,1 74.78925295941542,41.57341522824434,0 34.1836400264419,75.2377203360134,0 83.90239366249155,56.30804621605327,1 51.54772026906181,46.85629026349976,0 94.44336776917852,65.56892160559052,1 82.36875375713919,40.61825515970618,0 51.04775177128865,45.82270145776001,0 62.22267576120188,52.06099194836679,0 77.19303492601364,70.45820000180959,1 97.77159928000232,86.7278223300282,1 62.07306379667647,96.76882412413983,1 91.56497449807442,88.69629254546599,1 79.94481794066932,74.16311935043758,1 99.2725269292572,60.99903099844988,1 90.54671411399852,43.39060180650027,1 34.52451385320009,60.39634245837173,0 50.2864961189907,49.80453881323059,0 49.58667721632031,59.80895099453265,0 97.64563396007767,68.86157272420604,1 32.57720016809309,95.59854761387875,0 74.24869136721598,69.82457122657193,1 71.79646205863379,78.45356224515052,1 75.3956114656803,85.75993667331619,1 35.28611281526193,47.02051394723416,0 56.25381749711624,39.26147251058019,0 30.05882244669796,49.59297386723685,0 44.66826172480893,66.45008614558913,0 66.56089447242954,41.09209807936973,0 40.45755098375164,97.53518548909936,1 49.07256321908844,51.88321182073966,0 80.27957401466998,92.11606081344084,1 66.74671856944039,60.99139402740988,1 32.72283304060323,43.30717306430063,0 64.0393204150601,78.03168802018232,1 72.34649422579923,96.22759296761404,1 60.45788573918959,73.09499809758037,1 58.84095621726802,75.85844831279042,1 99.82785779692128,72.36925193383885,1 47.26426910848174,88.47586499559782,1 50.45815980285988,75.80985952982456,1 60.45555629271532,42.50840943572217,0 82.22666157785568,42.71987853716458,0 88.9138964166533,69.80378889835472,1 94.83450672430196,45.69430680250754,1 67.31925746917527,66.58935317747915,1 57.23870631569862,59.51428198012956,1 80.36675600171273,90.96014789746954,1 68.46852178591112,85.59430710452014,1 42.0754545384731,78.84478600148043,0 75.47770200533905,90.42453899753964,1 78.63542434898018,96.64742716885644,1 52.34800398794107,60.76950525602592,0 94.09433112516793,77.15910509073893,1 90.44855097096364,87.50879176484702,1 55.48216114069585,35.57070347228866,0 74.49269241843041,84.84513684930135,1 89.84580670720979,45.35828361091658,1 83.48916274498238,48.38028579728175,1 42.2617008099817,87.10385094025457,1 99.31500880510394,68.77540947206617,1 55.34001756003703,64.9319380069486,1 74.77589300092767,89.52981289513276,1
代码:
import time import numpy as np import numpy.random import pandas as pd import matplotlib.pyplot as plt import os # 读取本地e盘一个记录成绩的文本(随机生成的一堆数字) path = ‘e:\data.txt‘ # 两次考试成绩和是否被录取 pdData = pd.read_csv(path, header=None, names=[‘Exam1‘, ‘Exam2‘, ‘Admitted‘]) ‘‘‘ print(pdData.shape) (100, 3) 获得数据的维度(100行3列) 说明现在一共有100条数据 ‘‘‘ ‘‘‘ # 这里画一张图,大概观察下数据(见图1) positive = pdData[pdData[‘Admitted‘] == 1] negative = pdData[pdData[‘Admitted‘] == 0] fig, ax = plt.subplots(figsize=(10, 5)) ax.scatter(positive[‘Exam1‘], positive[‘Exam2‘], s=30, c=‘b‘, marker=‘o‘, label=‘Admitted‘) ax.scatter(negative[‘Exam1‘], negative[‘Exam2‘], s=30, c=‘r‘, marker=‘x‘, label=‘Not Admitted‘) ax.legend() ax.set_xlabel(‘Exam1 Score‘) ax.set_ylabel(‘Exam2 Score‘) #plt.show() ‘‘‘ # 定义sigmoid函数 def sigmoid(z): return 1 / (1 + np.exp(-z)) ‘‘‘ # 可以画sigmoid函数图形观察(图2): nums = np.arange(-10, 10, step=1) fig, ax = plt.subplots(figsize=(12, 4)) ax.plot(nums, sigmoid(nums), ‘b‘) plt.show() ‘‘‘ # 预测函数 def model(X, theta): return sigmoid(np.dot(X, theta.T)) # 添加一列:全为1 pdData.insert(0, ‘Ones‘, 1) orig_data = pdData.as_matrix() cols = orig_data.shape[1] X = orig_data[:, 0:cols - 1] y = orig_data[:, cols - 1:cols] theta = np.zeros([1, 3]) # 定义损失函数 def cost(X, y, theta): left = np.multiply(-y, np.log(model(X, theta))) right = np.multiply(1 - y, np.log(1 - model(X, theta))) return np.sum(left - right) / (len(X)) # 计算梯度 def gradient(X, y, theta): grad = np.zeros(theta.shape) error = (model(X, theta) - y).ravel() for j in range(len(theta.ravel())): # for each parmeter term = np.multiply(error, X[:, j]) grad[0, j] = np.sum(term) / len(X) return grad STOP_ITER = 0 STOP_COST = 1 STOP_GRAD = 2 def stopCriterion(type, value, threshold): # 设定三种不同的停止策略 if type == STOP_ITER: return value > threshold elif type == STOP_COST: return abs(value[-1] - value[-2]) < threshold elif type == STOP_GRAD: return np.linalg.norm(value) < threshold # 洗牌 def shuffleData(data): np.random.shuffle(data) cols = data.shape[1] X = data[:, 0:cols - 1] y = data[:, cols - 1:] return X, y def descent(data, theta, batchSize, stopType, thresh, alpha): # 梯度下降求解 init_time = time.time() i = 0 # 迭代次数 k = 0 # batch X, y = shuffleData(data) grad = np.zeros(theta.shape) # 计算的梯度 costs = [cost(X, y, theta)] # 损失值 while True: grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta) k += batchSize # 取batch数量个数据 if k >= n: k = 0 X, y = shuffleData(data) # 重新洗牌 theta = theta - alpha * grad # 参数更新 costs.append(cost(X, y, theta)) # 计算新的损失 i += 1 if stopType == STOP_ITER: value = i elif stopType == STOP_COST: value = costs elif stopType == STOP_GRAD: value = grad if stopCriterion(stopType, value, thresh): break return theta, i - 1, costs, grad, time.time() - init_time def runExpe(data, theta, batchSize, stopType, thresh, alpha): theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha) name = "Original" if (data[:, 1] > 2).sum() > 1 else "Scaled" name += " data - learning rate: {} - ".format(alpha) if batchSize == n: strDescType = "Gradient" elif batchSize == 1: strDescType = "Stochastic" else: strDescType = "Mini-batch ({})".format(batchSize) name += strDescType + " descent - Stop: " if stopType == STOP_ITER: strStop = "{} iterations".format(thresh) elif stopType == STOP_COST: strStop = "costs change < {}".format(thresh) else: strStop = "gradient norm < {}".format(thresh) name += strStop print("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format( name, theta, iter, costs[-1], dur)) fig, ax = plt.subplots(figsize=(12, 4)) ax.plot(np.arange(len(costs)), costs, ‘r‘) ax.set_xlabel(‘Iterations‘) ax.set_ylabel(‘Cost‘) ax.set_title(name.upper() + ‘ - Error vs. Iteration‘) return theta # 选择的梯度下降方法是基于所有样本的 n = 100 # 设定迭代次数(图3) runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001) # 根据损失值停止(图4) runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001) # 根据梯度变化停止(图5) runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001) # plt.show()
图1
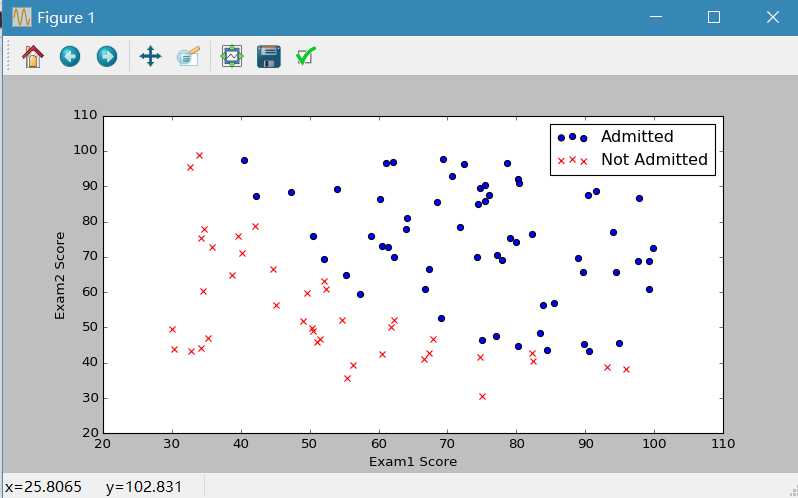
图2
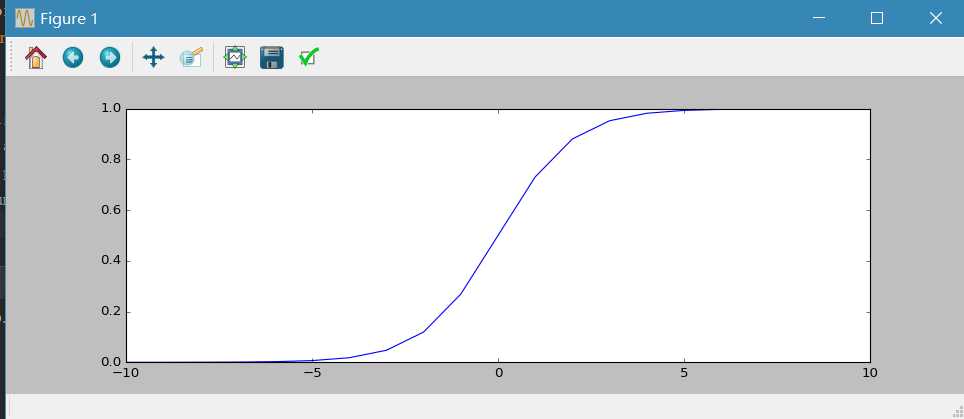
图3:
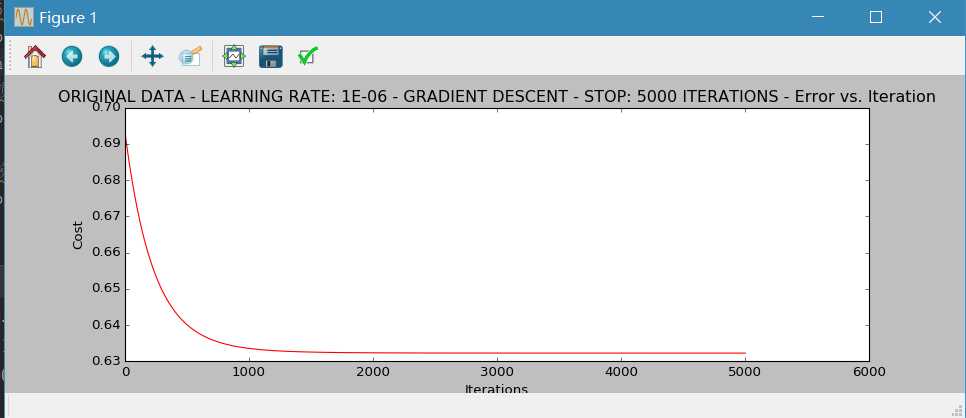
图4:
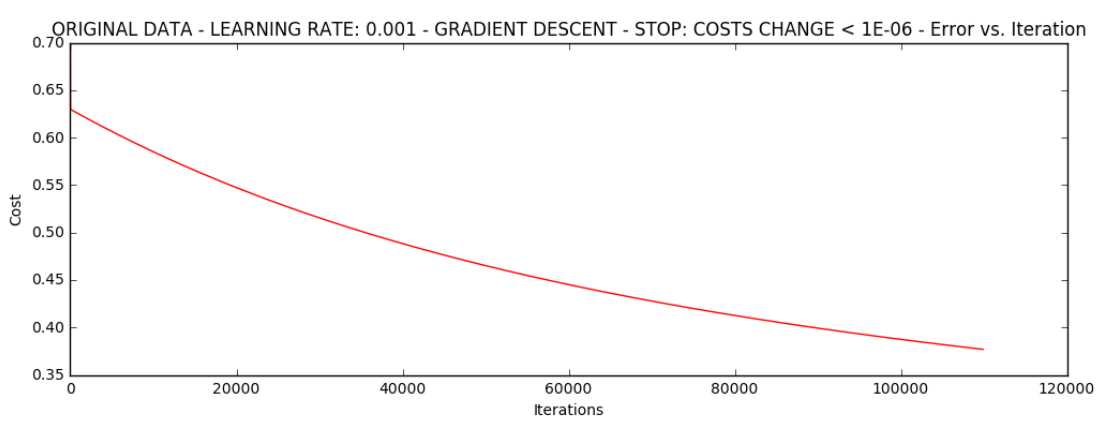
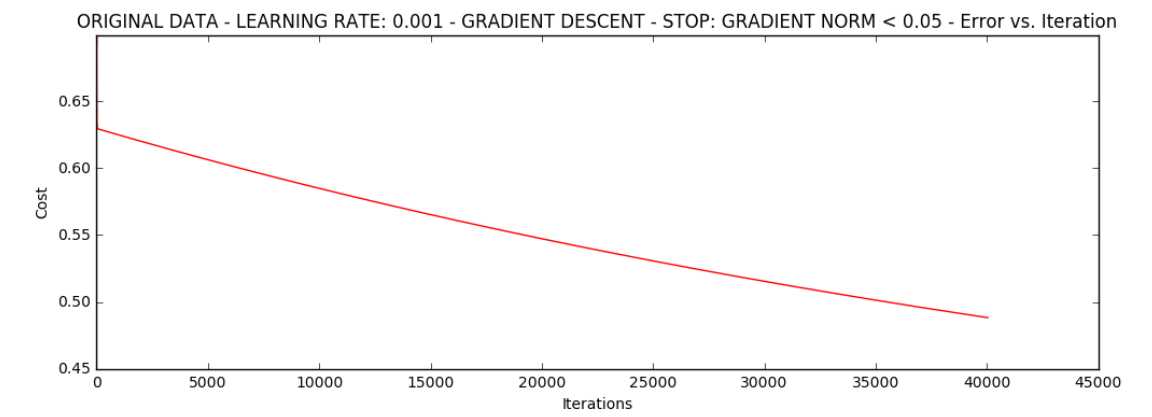
图5:
精度:
from sklearn import preprocessing as pp scaled_data = orig_data.copy() scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3]) theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002/5, alpha=0.001) def predict(X, theta): return [1 if x >= 0.5 else 0 for x in model(X, theta)] scaled_X = scaled_data[:, :3] y = scaled_data[:, 3] predictions = predict(scaled_X, theta) correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)] accuracy = (sum(map(int, correct)) % len(correct)) print(‘accuracy = {0}%‘.format(accuracy)) #最后结论:accuracy = 89%
