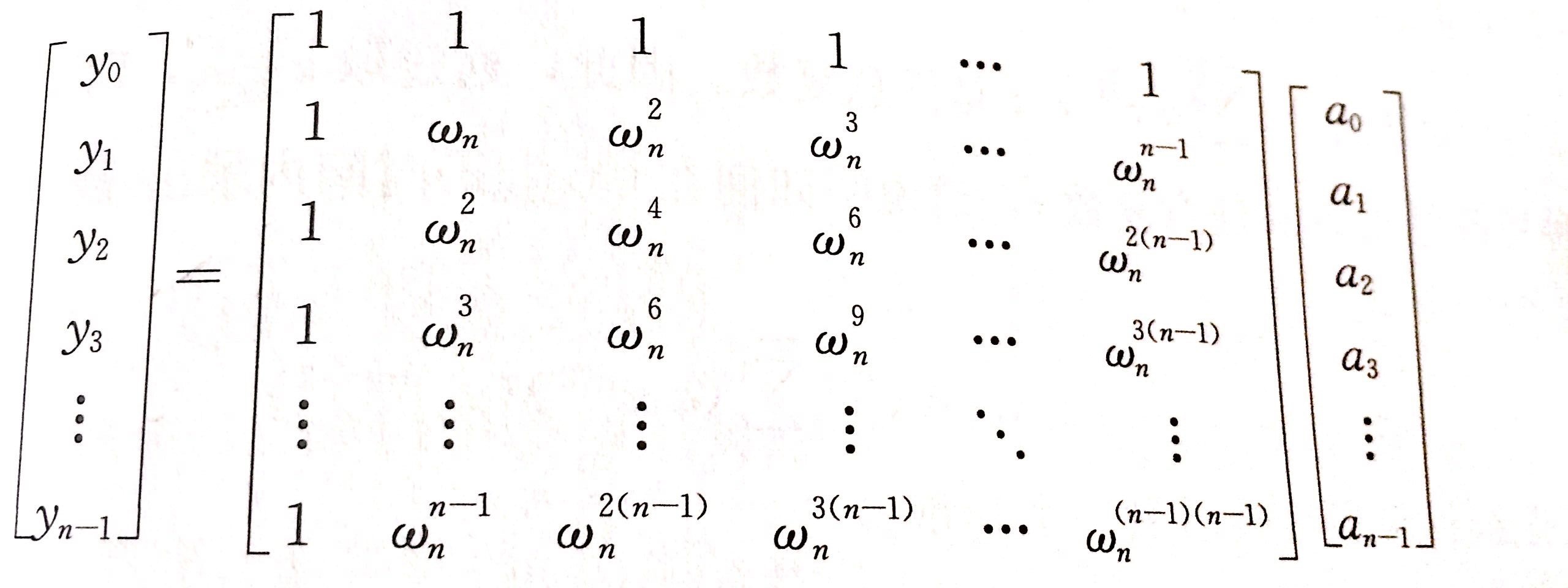参考博客:
https://blog.csdn.net/ggn_2015/article/details/68922404
https://blog.csdn.net/leo_h1104/article/details/51615710
fft->快速傅里叶变换,多项式乘法,即系数相乘,朴素的算法O(n^2),fft就是用来加速多项式乘法的,复杂度能达到O(nlogn)
几个基本概念:dft是离散傅里叶变换,idft是离散傅里叶反变换,虚数->a+bi,单位根即x^n=1的解,记为wn,共有n个解w(n,0)...w(n,n-1)
虚数 的几点性质:w(2n,2m)=w(n,m),w(n,k)=-w(n,k+n/2)
例如现有方程f(x)=a0+a1*x+...+an*x^n,g(x)=b0+b1*x+...+bn*x^n;
系数表示法就是指用{a0,a1...an}来表示整个方程,点值表示法就是用n个点例如{(x0,f(x0)),(x1,f(x1)...(xn,f(xn)))}来表示整个方程,可以证明n个点可以确定该方程.
在点值表示法的条件下,f(x)和g(x)相乘只需要y值相乘即可(x值必须相同).点值表示法的相乘结果就是((x0,f(x0)*g(x0)),.....(xn,f(xn)*g(xn))
整个计算过程就是将系数表示法用dft转换成点值表示法,然后点值表示法在O(n)的时间内算出两个多项式相乘的结果,然后用idft将结果转化成系数表示法
转换过程:
由于f(x)=a0+...+an*x^n,那么f(x)=a0+a2*x^2+...+an-1x^(n-1)+a1*x+a3*x^3+...+an*x^n;
然后f(x)=a0+a2*x^2+...+an-1*x^(n-1)+x*(a1+a3*x^2+...+an*x^(n-1)),
f(x)=p(x^2)+x*q(x^2) p(x)=a0+a2x+...,q(x)=a1+a3*x+...
就这样利用分治的思想,不断递归下去就得到了解,点值表示法选的点是1到n的单位根,(一定要保证系数个数是2的幂次)
递归计算时首先应该搞清楚乘的系数是什么,我们仔细观察一下,递归到最后每个系数到哪了
000 001 010 011 100 101 011 111(转换前的二进制表示)
0 1 2 3 4 5 6 7
0 2 4 6 1 3 5 7
0 4 2 6 1 5 3 7
000 100 010 110 001 101 011 111(转换后的二进制表示)
观察可以发现,递归到最后的时候每一项乘的都是二进制反转后的结果
代码:bit是位数,rev表示反转后指向的结果,
for(int i=0;i<(1<<bit);i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
假设现在rev[i]的二进制是abcd,没有操作之前的rev[i>>1]是0abc,操作之后的是cba0,再右移是0cba,再判断原来的d是不是1在最高位放1或0,就刚好是反转的结果
然后是迭代求点值表示法的结果
当w(n,k)中k<=n/2时,直接套用x^2=w(n,k)^2=w(n,2*k)=w(n/2,w)
当k>n/2时,有w(n,k)=w(n,k-n/2),x^2=w(n,k-n/2)^2=w(n/2,k-n/2),这样算出w(n/2)可以递推w(n)
cd wn=exp(cd(0,dft*pi/step));//单位根的解
从最底层开始倍增的迭代下去就好了
cd x=a[k];//上文的p(x) cd y=wnk*a[k+step];//q(x)*x a[k]=x+y;//f(x) a[k+step]=x-y;//对应的解wx在实虚轴上转了半圈
//蝴蝶操作
根据e^(2πi)=1,w[k]就是e^(2πi/k),这样整个dft过程就完成了,整个过程就是下图从(a0,...an-1)到(y0....yn-1)的过程
然后O(n)的多项式乘值,最后反向迭代idft,如图这个矩阵(y0,...yn-1)就是最后的dft之后的结果,idft就只需要乘上转化矩阵的逆矩阵即可
逆矩阵刚好是每个值的倒数/n(证明:我也不会= =)
最后放上a*b的高精度fft求法

//#pragma comment(linker, "/stack:200000000") //#pragma GCC optimize("Ofast,no-stack-protector") //#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native") //#pragma GCC optimize("unroll-loops") #include<bits/stdc++.h> #define fi first #define se second #define mp make_pair #define pb push_back #define pi acos(-1.0) #define ll long long #define mod (1000000007) #define C 0.5772156649 #define ls l,m,rt<<1 #define rs m+1,r,rt<<1|1 #define pil pair<int,ll> #define pii pair<int,int> #define cd complex<double> #define ull unsigned long long #define base 1000000000000000000 #define fio ios::sync_with_stdio(false);cin.tie(0) using namespace std; const double g=10.0,eps=1e-12; const int N=200000+10,maxn=1200000+10,inf=0x3f3f3f3f,INF=0x3f3f3f3f3f3f3f3f; cd a[N],b[N]; int rev[N]; void getrev(int bit) { for(int i=0;i<(1<<bit);i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1)); } void fft(cd* a,int n,int dft) { for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]); for(int step=1;step<n;step<<=1) { cd wn=exp(cd(0,dft*pi/step)); for(int j=0;j<n;j+=step<<1) { cd wnk(1,0); for(int k=j;k<j+step;k++) { cd x=a[k]; cd y=wnk*a[k+step]; a[k]=x+y; a[k+step]=x-y; wnk*=wn; } } } if(dft==-1)for(int i=0;i<n;i++)a[i]/=n; } char s[N],p[N]; int ans[N]; int main() { while(~scanf("%s",s)) { // memset(ans,0,sizeof ans); int sa=0,lena=strlen(s); while((1<<sa)<lena)sa++; scanf("%s",p); int sb=0,lenb=strlen(p); while((1<<sb)<lenb)sb++; int len=(1<<(max(sa,sb)+1)); for(int i=0;i<len;i++) { if(i<lena)a[i]=(double)s[lena-1-i]-‘0‘; else a[i]=0; if(i<lenb)b[i]=(double)p[lenb-1-i]-‘0‘; else b[i]=0; // printf("%f %f\n",a[i].real(),b[i].real()); } getrev(max(sa,sb)+1); fft(a,len,1);fft(b,len,1); for(int i=0;i<len;i++)a[i]=a[i]*b[i]; fft(a,len,-1); for(int i=0;i<len;i++)ans[i]=(int)(a[i].real()+0.5); // for(int i=0;i<len;i++)printf("%d\n",ans[i]); for(int i=0;i<len-1;i++)ans[i+1]+=ans[i]/10,ans[i]%=10; bool f=0; for(int i=len-1;i>=0;i--) { if(ans[i])printf("%d",ans[i]),f=1; else if(f||i==0)printf("0"); } puts(""); } return 0; } /******************** ********************/