题面
Sol
显然是求这样一个东西
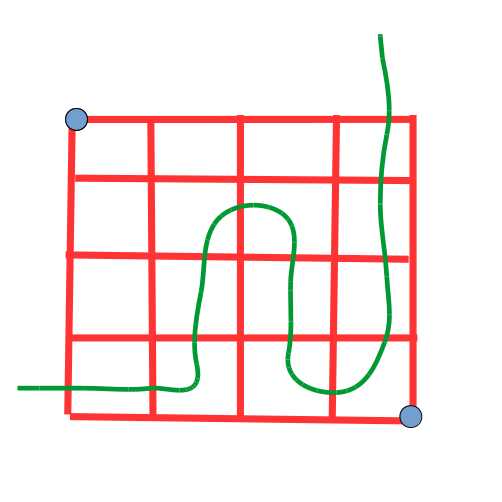
绿色的线为分割线,左上海拔为\(0\),右下为\(1\)
分隔线经过的边就是贡献的答案
那么这就是平面图最小割,转成对偶图求最短路就好了
\(SPFA\)真心慢,以后还是跑\(Dijstra\)
# include <bits/stdc++.h>
# define RG register
# define IL inline
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(1e6 + 5);
typedef int Arr[_];
IL int Input(){
RG int x = 0, z = 1; RG char c = getchar();
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
return x * z;
}
int n, cnt, S, T, id[505][505], num;
Arr dis, vis, first;
struct Edge{
int to, next, w;
} edge[_ << 1];
queue <int> Q;
IL void Add(RG int u, RG int v, RG int w){
edge[cnt] = (Edge){v, first[u], w}, first[u] = cnt++;
}
IL int SPFA(){
Fill(dis, 127); dis[S] = 0;
vis[S] = 1; Q.push(S);
while(!Q.empty()){
RG int u = Q.front(); Q.pop();
for(RG int e = first[u]; e != -1; e = edge[e].next){
RG int w = edge[e].w, v = edge[e].to;
if(dis[u] + w < dis[v]){
dis[v] = dis[u] + w;
if(!vis[v]) vis[v] = 1, Q.push(v);
}
}
vis[u] = 0;
}
return dis[T];
}
int main(RG int argc, RG char* argv[]){
Fill(first, -1), n = Input();
for(RG int i = 1; i <= n; ++i)
for(RG int j = 1; j <= n; ++j)
id[i][j] = ++num;
T = num + 1; RG int r = n + 1;
for(RG int i = 1; i <= r; ++i)
for(RG int j = 1; j <= n; ++j){
RG int v = Input();
if(i == 1) Add(id[i][j], T, v);
else if(i == r) Add(S, id[i - 1][j], v);
else Add(id[i][j], id[i - 1][j], v);
}
for(RG int i = 1; i <= n; ++i)
for(RG int j = 1; j <= r; ++j){
RG int v = Input();
if(j == 1) Add(S, id[i][j], v);
else if(j == r) Add(id[i][j - 1], T, v);
else Add(id[i][j - 1], id[i][j], v);
}
for(RG int i = 1; i <= r; ++i)
for(RG int j = 1; j <= n; ++j){
RG int v = Input();
if(i == 1) Add(T, id[i][j], v);
else if(i == r) Add(id[i - 1][j], S, v);
else Add(id[i - 1][j], id[i][j], v);
}
for(RG int i = 1; i <= n; ++i)
for(RG int j = 1; j <= r; ++j){
RG int v = Input();
if(j == 1) Add(id[i][j], S, v);
else if(j == r) Add(T, id[i][j - 1], v);
else Add(id[i][j], id[i][j - 1], v);
}
printf("%d\n", SPFA());
return 0;
}