1.需求分析
1. 使用 -n 参数控制生成题目的个数,例如 Myapp.exe -n 10 -o Exercise.txt 将生成10个题目。 2. 使用 -r 参数控制题目中数值(自然数、真分数和真分数分母)的范围,例如 Myapp.exe -r 10 将生成10以内(不包括10)的四则运算题目。该参数可以设置为1或其他自然数。该参数必须给定,否则程序报错并给出帮助信息。 3. 生成的题目中如果存在形如e1 ÷ e2的子表达式,那么其结果应是真分数。 4. 每道题目中出现的运算符个数不超过3个。 5. 程序一次运行生成的题目不能重复,即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。例如,23 + 45 = 和45 + 23 = 是重复的题目,6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的,由于+是左结合的,1+2+3等价于(1+2)+3,也就是3+(1+2),也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题,因为1+2+3等价于(1+2)+3,而3+2+1等价于(3+2)+1,它们之间不能通过有限次交换变成同一个题目。 生成的题目存入执行程序的当前目录下的Exercises.txt文件,格式如下: 1. 四则运算题目1 2. 四则运算题目2 …… 其中真分数在输入输出时采用如下格式,真分数五分之三表示为3/5,真分数二又八分之三表示为2’3/8。 6. 在生成题目的同时,计算出所有题目的答案,并存入执行程序的当前目录下的Answers.txt文件,格式如下: 1. 答案1 2. 答案2 特别的,真分数的运算如下例所示:1/6 + 1/8 = 7/24。 7. 程序应能支持一万道题目的生成。 8. 程序支持对给定的题目文件和答案文件,判定答案中的对错并进行数量统计,并会输出所有题目中重复的题目,输入参数如下: Myapp.exe -e <exercisefile>.txt -a <answerfile>.txt -o Grade.txt 统计结果输出到文件Grade.txt,格式如下: Correct: 5 (1, 3, 5, 7, 9) Wrong: 5 (2, 4, 6, 8, 10) Repeat:2 RepeatDetail: (1) 2,45+32 Repeat 3,32+45 (2) 5,3+(2+1) Repeat 7,1+2+3 解释: Correct: 5 ----5道题目正确,正确的题号 1,3,5,7,9 Wrong:5 -----5道题目错误,错误的题号 2,4,6,8,10 Repeat:2 2---组题目重复 (1) 第一组 题号2,题目 45+32 与题号3的题目重复,题号3为 32+45 (2)第二组 题号5,题目 3+(2+1) 与题号7的题目重复,题号7为 1+2+3 其中“:”后面的数字5表示对/错的题目的数量,括号内的是对/错题目的编号。为简单起见,假设输入的题目都是按照顺序编号的符合规范的题目。
2.功能设计
-
基本功能
a.生成多个四则运算算式
b.校验计算结果
-
拓展功能
a.四则运算含3个以内运算符
b.能输出直观的题目(合理去括号)
c.计算结果为真分数
d.计算的数字有规定范围
e.生成的算式合法(不含除以0或分母为0)
f.对计算结果进行通分化简
g.批改支持将丢失的题目添加进错误
-
高级功能
a.支持任意多个运算符
b.二叉树查重
3.设计实现
question:
-->Calculation.java:根据二叉树根节点计算答案,包含化简
-->CreateQuestion.java:生成二叉树算式,包含查重及合法校验
-->Number.java:数的存储格式,包含整数部分、分子部分、分母部分
start:
-->OutQuestion.java:输入参数操作、文件输入输出操作
tree:
-->BinaryTree.java:二叉树,包含转化为String算式的函数
-->TreeNode:树的节点
4.代码说明
-
递归查重

//---------------------------------------------------------------------------------- //代码功能:递归实现二叉树查重 //---------------------------------------------------------------------------------- //实现思路: //1、先判断两个算式答案相不相同,不相同则算式一定不相同。 //2、然后对两式计算左右两边的值是否能匹配上。 //3、若能,将其子节点匹配后递归回1再比较,重复123操作,直到结束或返回不同。 //---------------------------------------------------------------------------------- private boolean isRepeat(List<BinaryTree> questions, BinaryTree ques) { // 先按答案查重节省时间,再详细对比 for (BinaryTree bt : questions) { if (bt.getAnswer() == ques.getAnswer()) { if (isRepeatTree(bt.getRootNode(), ques.getRootNode())) { System.out.println("重复:【" + bt.getQuestion() + "】【" + ques.getQuestion() + "】");// 输出重复问题 return true; } } } return false; } private boolean isRepeatTree(TreeNode tnode1, TreeNode tnode2) {// 两棵树详细对比查重 if (tnode1.getData().equals(tnode2.getData())) {// 当前节点相同 if (tnode1.getLeftTreeNode() == null && tnode2.getLeftTreeNode() == null) { // 两树均无下节点 return true; } String l1, r1, l2, r2; l1 = Calculation.calculation(tnode1.getLeftTreeNode()).getData(); r1 = Calculation.calculation(tnode1.getRightTreeNode()).getData(); l2 = Calculation.calculation(tnode2.getLeftTreeNode()).getData(); r2 = Calculation.calculation(tnode2.getRightTreeNode()).getData(); if (!(l1.equals(r1) && l2.equals(r2) && l1.equals(l2))) {// 两个节点的左右节点计算值不全相同,非(a,a)和(a,a)这种组合 if (l1.equals(l2) && r1.equals(r2)) { // 同一边的相同 return isRepeatTree(tnode1.getLeftTreeNode(), tnode2.getLeftTreeNode()) && isRepeatTree(tnode1.getRightTreeNode(), tnode2.getRightTreeNode()); } else if (l1.equals(r2) && r1.equals(l2)) { // 不同边的相同 return isRepeatTree(tnode1.getLeftTreeNode(), tnode2.getRightTreeNode()) && isRepeatTree(tnode1.getRightTreeNode(), tnode2.getLeftTreeNode()); } return false;// 不相同 } else { // 像(2,2)和(2,2)这种组合 return (isRepeatTree(tnode1.getLeftTreeNode(), tnode2.getLeftTreeNode()) && isRepeatTree(tnode1.getRightTreeNode(), tnode2.getRightTreeNode()) || isRepeatTree( tnode1.getLeftTreeNode(), tnode2.getRightTreeNode()) && isRepeatTree(tnode1.getRightTreeNode(), tnode2.getLeftTreeNode()));// 有一种完全匹配即可 } } else { return false; } }
-
输出算式

//------------------------------------- //功能:根据二叉树根节点输出算式 //------------------------------------- public String toString() { // 中序遍历输出算式带括号 String result = inorderTraversal(rootNode); return result; } private String inorderTraversal(TreeNode tnode) { // 中序遍历递归算法,默认左右节点同时存在或同时不存在 if (tnode.getLeftTreeNode() != null && tnode.getRightTreeNode() != null) { return addBracketsL(tnode, tnode.getLeftTreeNode()) + tnode.getData() + addBracketsR(tnode, tnode.getRightTreeNode());// addBrackets添加括号前会判断 } else { return tnode.getData(); } } private String addBracketsL(TreeNode f, TreeNode c) { // 递归路径:inorderTraversal->addBracketsL(或R)->inorderTraversal if ((f.getData() == "*" || f.getData() == "÷") && (c.getData() == "+" || c.getData() == "-")) { return "(" + inorderTraversal(c) + ")"; } else { return inorderTraversal(c); } } private String addBracketsR(TreeNode f, TreeNode c) { if ((f.getData() == "*" || f.getData() == "÷") && (c.getData() == "+" || c.getData() == "-")) { return "(" + inorderTraversal(c) + ")"; } else if (f.getData() == "-" && (c.getData() == "+" || c.getData() == "-")) { // 减号后面的加减号要加括号,如:1-(2+3)、1-(2-3) return "(" + inorderTraversal(c) + ")"; } else if (f.getData() == "÷" && (c.getData() == "*" || c.getData() == "/")) { // 除号后面的乘除号要加括号,如:1÷(2x3)、1÷(2÷3) return "(" + inorderTraversal(c) + ")"; } else { return inorderTraversal(c); } }
5.测试运行
-
生成题目及答案
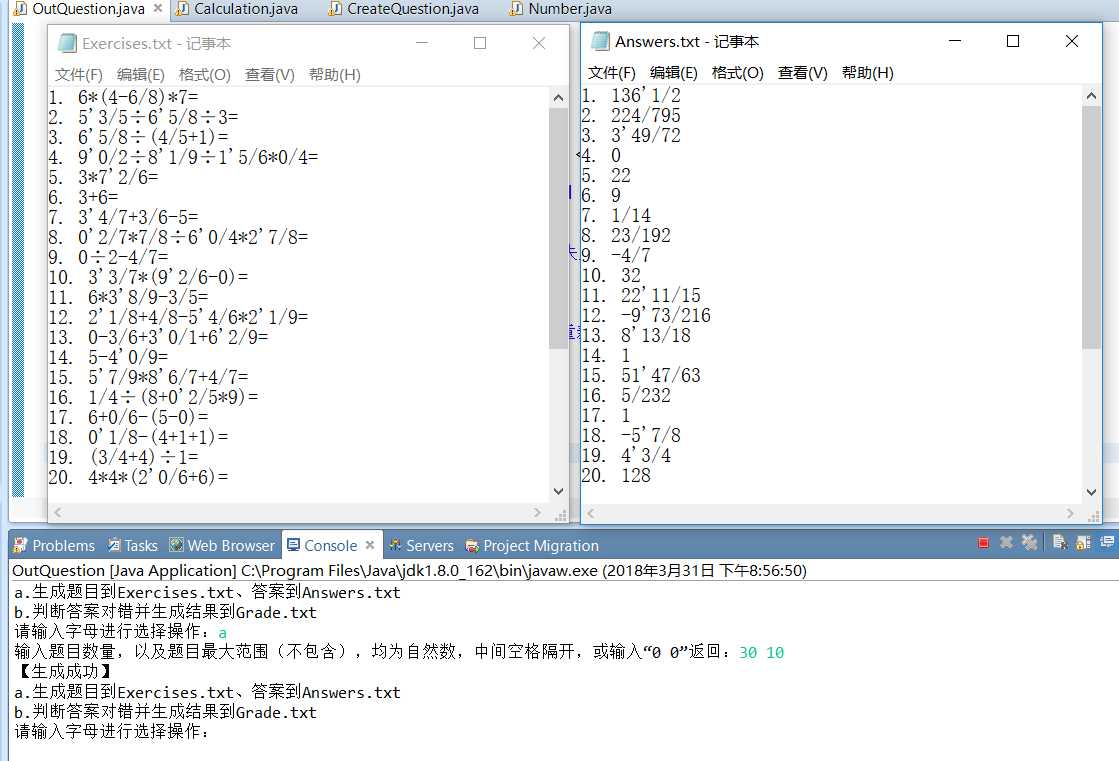
-
批改答案(删除问题行仍可判错)
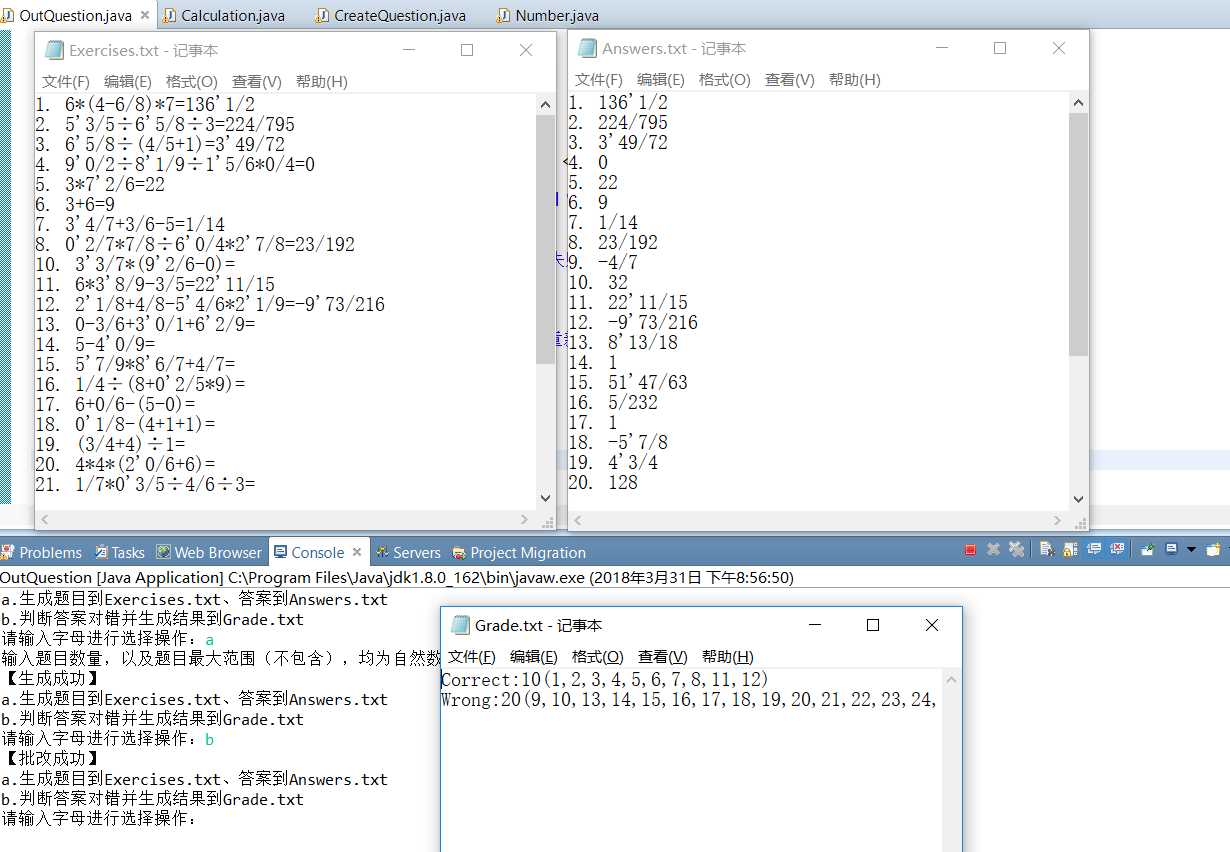
-
二叉树同构查重(生成时查重,若重复则舍弃,输出的题目无重复的)
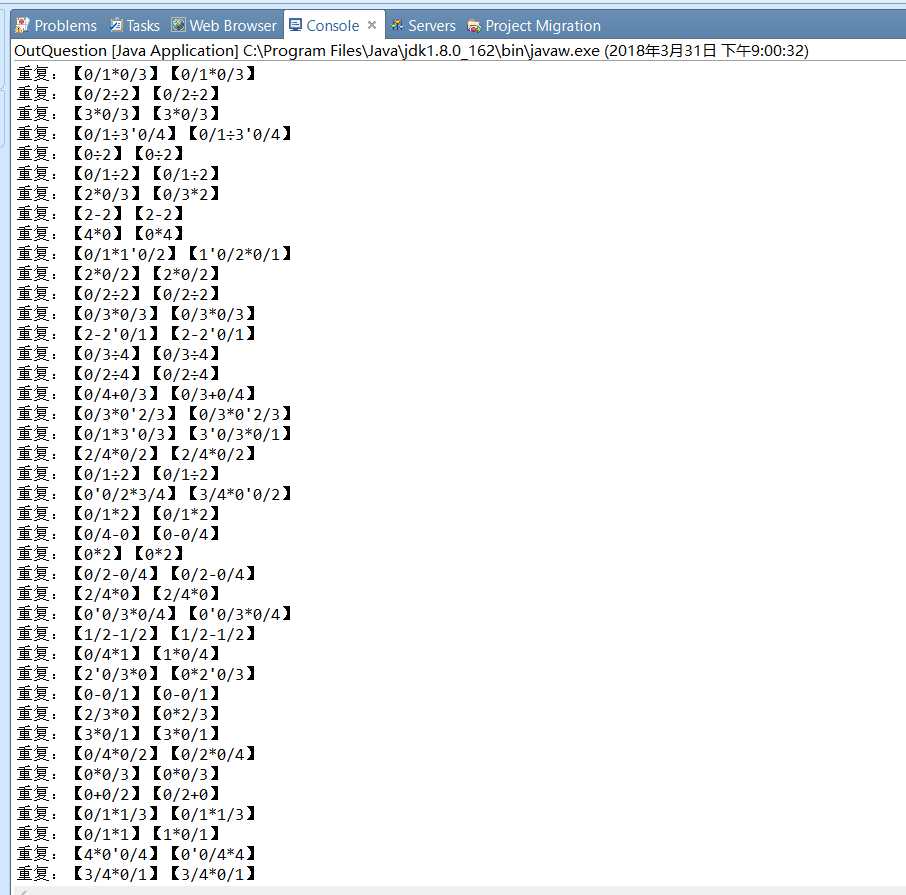
-
生成多个算式
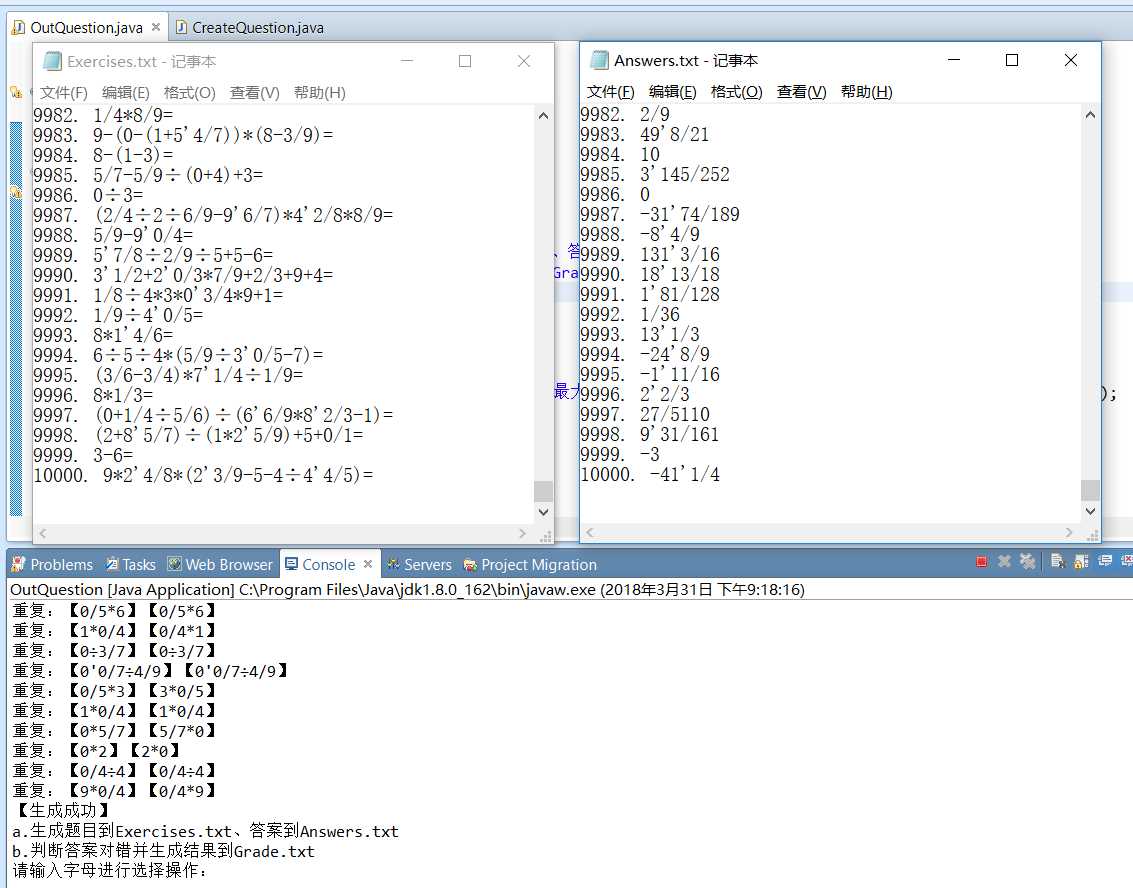
备注:代码写得比较赶,并未大量测试
完整代码:点击跳转

