一 Perception Hypothesis Set

1 A Simple Hypothesis Set: the ‘Perceptron‘

本节还是使用银行发信用卡的例子，银行掌握用户的年龄、年薪、工龄和负债情况。这里建立一个模型，每一个用户可以用一个向量来表示，每个用户的每一种信息可以当作向量的一个维度(x_i)。把每个用户的维度综合起来产生一个分数，分数超过标准就给信用卡。在计算时加上w_i来表示权重。

对计算后的结果，好的(可以发卡)表示+1，不好的(不能发卡)表示-1。刚好等于门槛值(threshold)的时候很少，可以忽略不计。

这里的h称作感知器(perceptron)，这是本节的主要内容。

2 Vector Form of Perceptron Hypothesis

此时可以对h(x)做一个数学上的转化，将-threshold当作w₀，引入一个x₀=+1与w₀相乘，数学表示方式被简化。公式如下图被简化为两个向量内积的形式，其中T表示转置。

3 Perceptions in R²

下面是一个二维图来说明感知机模型。w₀+w₁x₁+w₂x₂₌₀是平面上的一条线，线的一侧是好的情况(+1)，另一侧是坏的情况(-1)。每个用户的情况y用符号表示，圈表示好(+1)，叉表示坏(-1)。

perceptions在这个模型中就是一条直线，称为线性分类器[linear (binary) classifiers]。线性分类器也可以在更高维度。

二 Perception Learning Algorithm(PLA)

1 select g from H

这里我们设计一个演算法来寻找一条直线，使这条直线能将平面上的所有好坏分开，让这个g跟f几乎一模一样。

2 Perception Learning Algorithm(PLA)

一开始在二维平面中有一条会有一些错误的初始的线w₀(代表g₀)，然后逐步将线两侧错误的点修正，即移动线来完全修正或减轻错误，直到这条线达到了期望的效果才结束。

将data中的(x_n(t),y_n(t))做内积得到w_t，在验证时发现(w^T_tx_n(t))y_n(t) ，于是我们尝试进行纠正。如下图右侧。若要的内积是+结果做出来是-的，则向量w+x；若要的内积是-结果做出来是+的，则向量w-x

注：图中w为线的法向量

在用所有data进行验证时，可以用默认的正序也可以乱序，总之只要能转到所有data就好

3 Seeing is Believing

一个使用PLA算法的例子

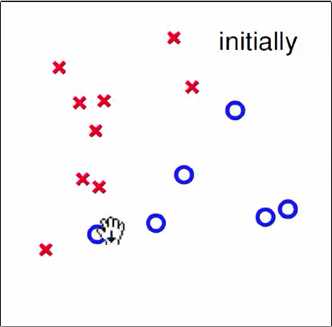
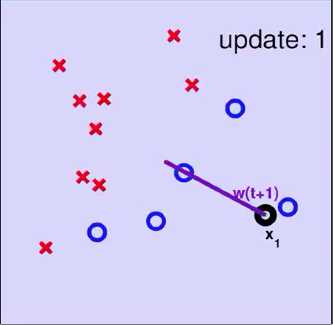
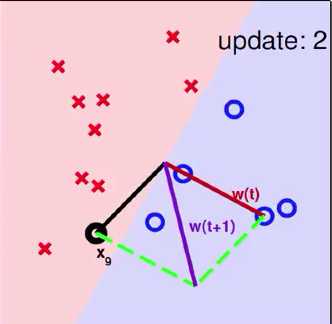
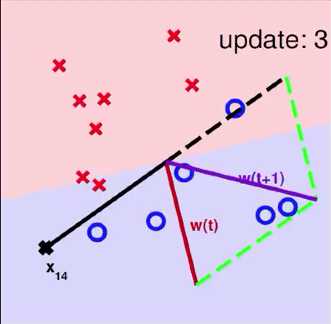
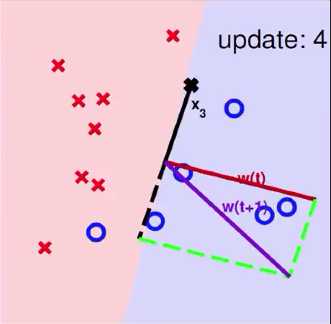
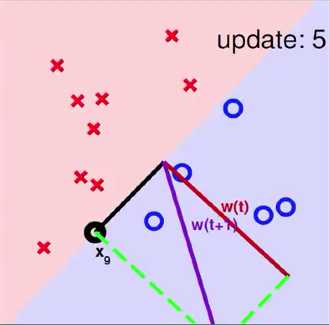
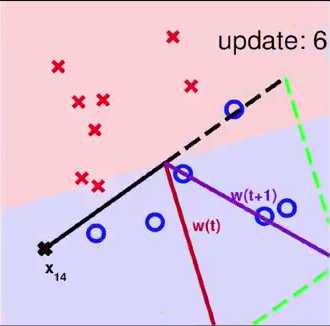
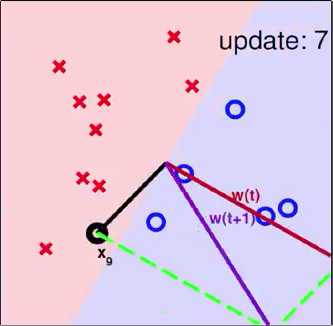
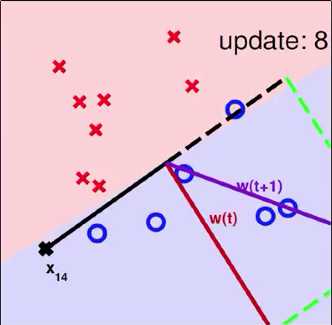
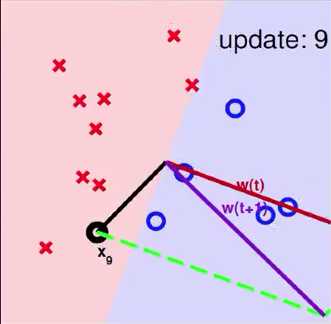
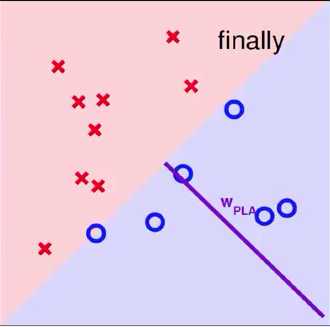
4 Some Remaining Issues of PLA

对于此算法仍然由问题需要思考

*PLA一定会停下来吗

*PLA的停下来结果对于没有使用的真是data是否真的满足g≈f，若没有停下来是否会有 g≈f

三 Guarantee of PLA

1 Linear Separability

*If PLA halts (i.e. no more mistakes), (necessary condition) D allows some w to make no mistakes

*Call such D linear separable(线性可分)

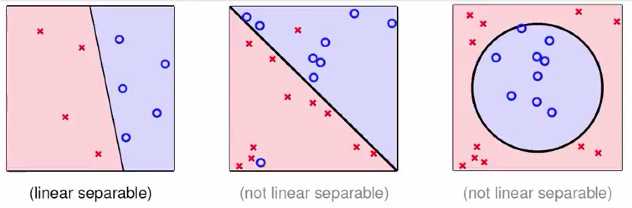
2 PLA Fact

w_t Gets More Aligned with w_f

线性可分时，必然满足以下

对任意的x_n

PLA会对每次错误的点进行修正，更新权重w_t+1的值，如果w_t+1与w_f越来越接近，数学运算上就是内积越大，那表示w_t+1是在接近目标权重w_f，证明PLA是有学习效果的。所以，计算w_t+1与w_f的内积：

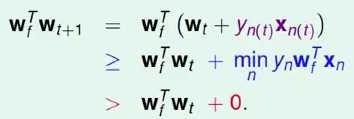
w_t Does Not Grow Too Fast

从推导可以看出，w_t+1与wf的内积跟wt与wf的内积相比更大了。似乎说明了w_t+1更接近w_f，但是内积更大，可能是向量长度更大了，不一定是向量间角度更小。所以，下一步，我们还需要证明w_t+1与w_t向量长度的关系

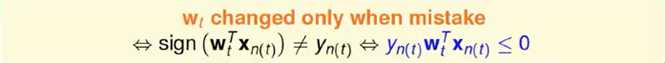
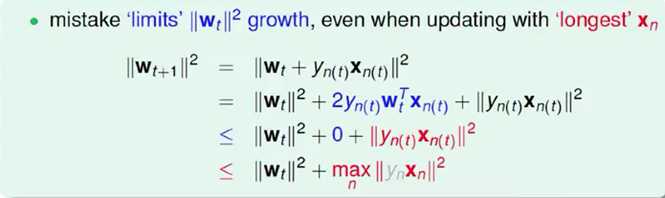
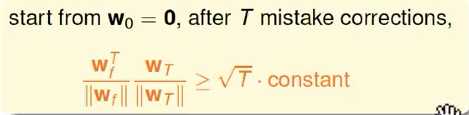
四 Non Separable Data

1 More About PLA

对于线性可分的情况，PLA能停下来并正确分类，然而线性不可分时，w_f实际上不存在，之前推到不成立，PLA不一定能停下来。所以PLA在使用时也有一些麻烦的地方。

2 Learning with Noisy Data

我们在机器学习中使用的data可能是有noisy data的，导致拿到的data不一定会是线性可分。这时的机器学习流程：

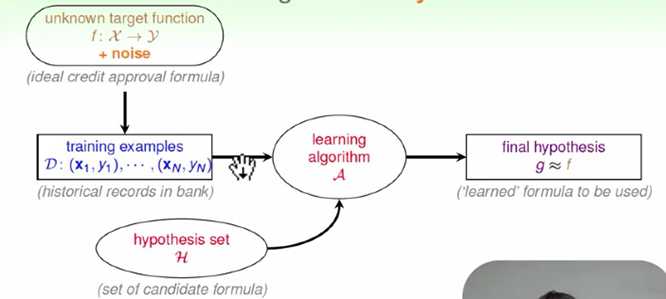
3 Line with Noise Tolerance

在有noise的情况下我们没有办法找到完全正确的线，所以我们转而去找犯的错误最少的线为g。

上面的做法是NP问题，但无法做到写成程序来实现。

4 Pocket Algorithm

我们对PLA算法进行修改，产生了Pocket Algorithm。它的算法流程与PLA相似，首先初始化权重w₀，计算出在这条初始化的直线中，分类错误点的个数，将这条直线放进口袋。然后进行修正，更新w，得到一条新的直线，再计算分类错误的点的个数，并与之前错误点个数比较，取个数较小的直线作为我们当前选择的分类直线，放进口袋替换。之后，再经过n次迭代，不断比较当前分类错误点个数与之前最少的错误点个数比较，选择最小的值的线留在口袋里。直到迭代次数完成后，选取个数最少的直线对应的w，即为我们最终想要得到的权重值，即口袋里最终的线。

5 Summary