---恢复内容开始---

因为感觉都比较难，所以果断选第一个题目

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n

例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

一，算法

描述：针对最大子段和这个具体问题本身的结构，我们还可以从算法设计的策略上对上述O(n^2)计算时间算法进行更进一步的改进。从问题的解结构也可以看出，它适合于用分治法求解。

如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和，则a[1:n]的最大子段和有三种情况：
（1） a[1:n]的最大子段和与a[1:n/2]的最大子段和相同
（2） a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同
（3） a[1:n]的最大子段和为a[i]+…+a[j]，并且1<=i<=n/2，n/2+1<=j<=n。
对于（1）和（2）两种情况可递归求得，但是对于情况（3），容易看出a[n/2]，a[n/2+1]在最大子段中。因此，我们可以在a[1:n/2]中计算出s1=max(a[n/2]+a[n/2-1]+…+a[i]),0<=i<=n/2，并在a[n/2+1:n]中计算出s2= max(a[n/2+1]+a[n/2+2]+…+a[i])，n/2+1<=i<=n。则s1+s2为出现情况（3）的最大子段和。

二，关键代码

#include

三，单元测试

覆盖方法
(1)语句覆盖：选择合适用例，所有语句被执行一次。
(2)判定覆盖：每个判定至少取一次真、一次假。
(3)条件覆盖：每个条件的各种可能结果至少满足一次。
(4)判定条件覆盖：同时满足判断覆盖和条件覆盖。
(5)条件组合覆盖：所有组合情况都要覆盖一次。
由于个人能力有限，所以选择使用Code Blocks

四，测试结果

用-2,11，-4,13，-5，-2
显示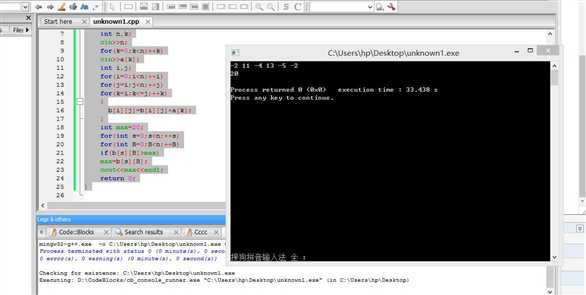

五，心得体会

感觉自己学的软件工程有点假，没学太懂，自己太笨，心累。

---恢复内容结束---