来自:某小皮
最优化函数库Optimization
优化是找到最小值或等式的数值解的问题。scipy.optimization子模块提供函数最小值,曲线拟合和寻找等式的跟的有用算法。
最小二乘拟合
假设有一组实验数据(xi, yi),事先知道它们之间应该满足某函数关系yi = f(xi),通过这些已知的信息,需要确定函数f的一些参数。例如,如果函数f是线性函数f(x) = kx + b,那么参数k和b就是需要确定的值。
如果用p表示函数中需要确定的参数,那么目标就是找到一组p,使下面的函数s的值最小:
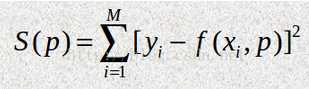
这种算法被称作最小二乘拟合(Least-square fitting)。
使用leastsq()进行最小二乘拟合计算。leastsq()只需要将计算误差的函数和待确定参数的初始值传递给它即可。
Leastsq()函数传入误差计算函数和初始值,该初始值将作为误差计算函数的第一个参数传入;
计算的结果r是一个包含两个元素的元组,第一个元素是一个数组,表示拟合后的参数k,b;第二个元素如果等于1,2,3,4中的其中一个整数,则拟合成功,否则将返回mesg。
示例:
使用最小二乘对带噪声的正弦波数据进行拟合:
拟合得到的参数虽然和实际的参数有可能完全不同,但是由于正弦函数具有周期性,实际上拟合的结果和实际的函数是一致的。
import numpy as np from scipy.optimize import leastsq def func(x, p):
数据拟合所用的函数:A*sin(2*pi*k*x + theta)
A, k, theta = p return A*np.sin(2*np.pi*k*x + theta) def residuals(p, y, x):
实验数据x, y和拟合函数之间的误差,p为拟合需要找到的系数
