传送门:https://www.luogu.org/problemnew/show/P2891
题面
 \
\
Solution
网络流
先引用一句真理:网络流最重要的就是建模
今天这道题让我深有体会
首先,观察数据范围,n=100,一般这种100-1000的图论题,很有可能是网络流.
那就直接从网络流的角度入手
考虑这样建模
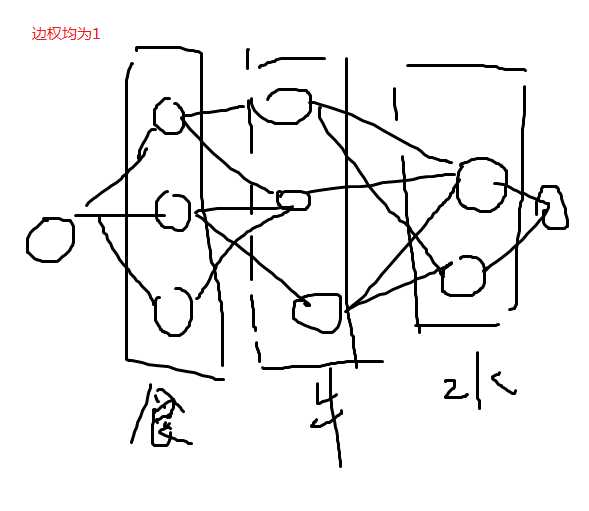
建模要点如下:
1.建权值为1的边,保证每个食物和水仅用一次
2.没了
对以上的图求一个最大流,那不就是我们想要的最大的匹配数吗?
看起来是不是很OjbK?
其实不然,这样子一头牛有可能脚踏N条食物和水,但是题目要求一头牛只能吃喝一次
反例如下:
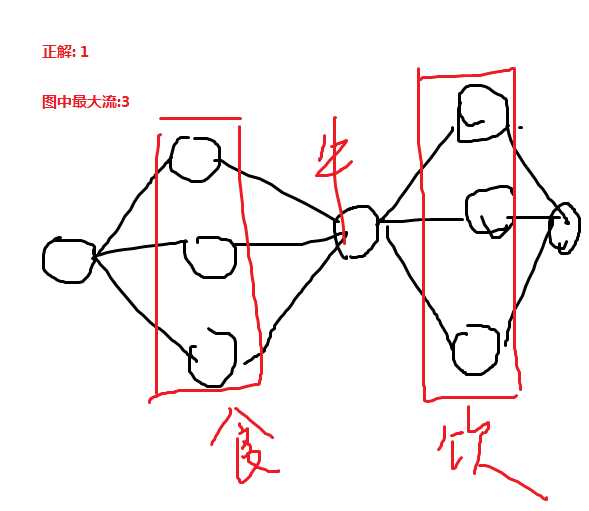
所以说,我们要对一头牛吃的东西做一个限制,保证其只流过1
怎么限制呢?
直接把一头牛拆成两头牛,中间连一条边就OK了嘛
如下图:
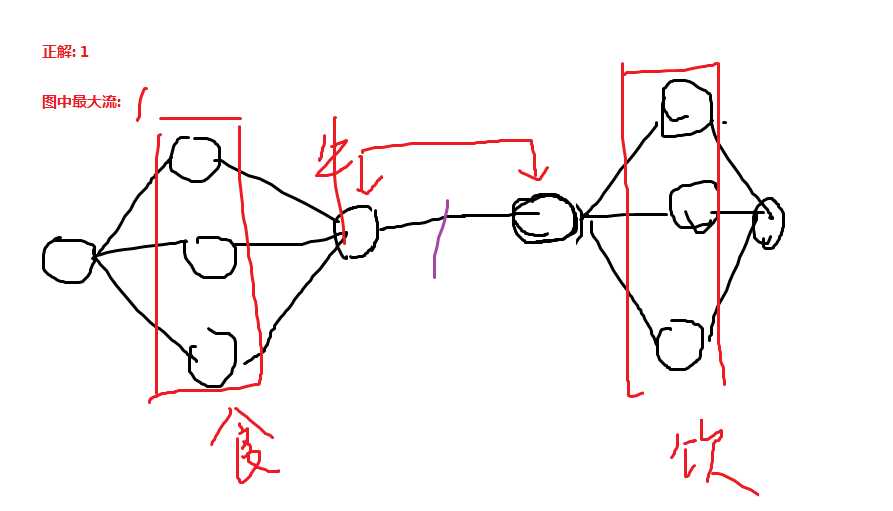
接下来就可以考虑如何给点编号了
我的编号方法很直接,很暴力
源点:1
食物: 2 ~ 2+f-1
牛 2+f ~ 2+f+2n -1
水: 2+f+2n ~ 2+f+2n+d
汇点:1000
如下图所示
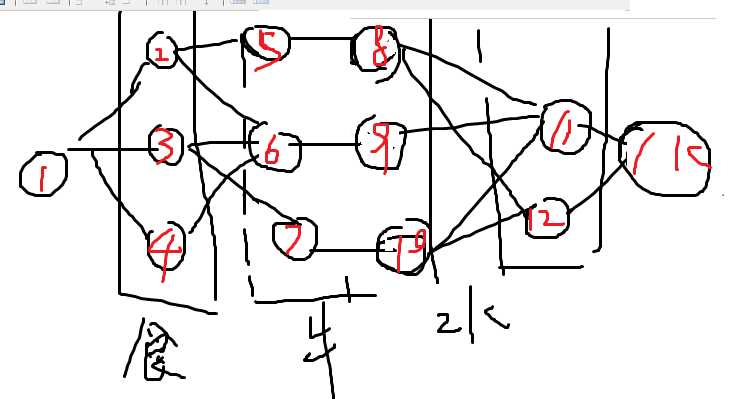
按照以上方法,每种物品对应的点为:
食物i : 1+i
牛i : 1+f+i
牛i的右边的分点: 1+f+n+i
水i: 1+f+2*n+i
然后dinic直接求一波最大流就可以带走啦
DINIC教程传送门: http://www.cnblogs.com/SYCstudio/p/7260613.html (个人感觉写得很清楚)
Code

//Luogu P2891 [USACO07OPEN]吃饭Dining //Apr,2ed,2018 //Dinic求最大流 #include<iostream> #include<cstdio> #include<vector> #include<cstring> using namespace std; long long read() { long long x=0,f=1; char c=getchar(); while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();} while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();} return x*f; } const int N=100+10; const int M=N*10; const int inf=0x3f3f3f3f; struct line { int t,rev,w; }; vector <line> e[M]; inline void AddLine(int s,int t) { line temp; temp.t=t,temp.rev=e[t].size(),temp.w=1; e[s].push_back(temp); temp.t=s,temp.rev=e[s].size()-1,temp.w=0; e[t].push_back(temp); } int n,f,d; int dl[M],head,tail,depth[M]; bool visited[M]; bool bfs() { memset(visited,0,sizeof visited); dl[1]=1,depth[1]=1; visited[1]=true; head=1,tail=2; while(head<tail) { int now=dl[head],size=e[now].size(); for(int i=0;i<size;i++) if(visited[e[now][i].t]==false and e[now][i].w>0) { visited[e[now][i].t]=true; dl[tail++]=e[now][i].t; depth[e[now][i].t]=depth[now]+1; } head++; } return visited[1000]; } int dfs(int now,int f) { if(now==1000) return f; int size=e[now].size(),ans=0; for(int i=0;i<size;i++) if(depth[e[now][i].t]==depth[now]+1 and e[now][i].w>0) { int t_ans=dfs(e[now][i].t,min(f,e[now][i].w)); e[now][i].w-=t_ans; e[e[now][i].t][e[now][i].rev].w+=t_ans; f-=t_ans,ans+=t_ans; if(f==0) break; } return ans; } int Dinic() { int ans=0; while(bfs()) ans+=dfs(1,inf); return ans; } int main() { n=read(),f=read(),d=read(); for(int i=1;i<=1000;i++) e[i].reserve(16); for(int i=1;i<=f;i++) AddLine(1,1+i); for(int i=1;i<=d;i++) AddLine(1+f+2*n+i,1000); for(int i=1;i<=n;i++) { int F=read(),D=read(),temp; for(int j=1;j<=F;j++) { temp=read(); AddLine(1+temp,1+f+i); } for(int j=1;j<=D;j++) { temp=read(); AddLine(1+f+n+i,1+f+2*n+temp); } } for(int i=1;i<=n;i++) AddLine(1+f+i,1+f+n+i); printf("%d",Dinic()); return 0; }
后记
写的时候发现自己真的有点生疏了,这种比较靠记忆的算法还是久不久搞一下来恢复记忆为妙
网络流的时间复杂度真玄学

