一、经验风险最小化
1、有限假设类情形
- 对于Chernoff bound 不等式，最直观的解释就是利用高斯分布的图象。而且这个结论和中心极限定律没有关系，当m为任意值时Chernoff bound均成立，但是中心极限定律不一定成立。
- 随着模型复杂度（如多项式的次数、假设类的大小等）的增长，训练误差逐渐降低，而一般误差先降低到最低点再重新增长。训练误差降低，是因为模型越复杂，对于训练集合的拟合就越好。对于一般误差，最左边的端点表示欠拟合（高偏差），最右边的端点表示过拟合（高方差），最小化一般误差时，一般倾向于选取中间的模型复杂度，最小一般误差的区域。
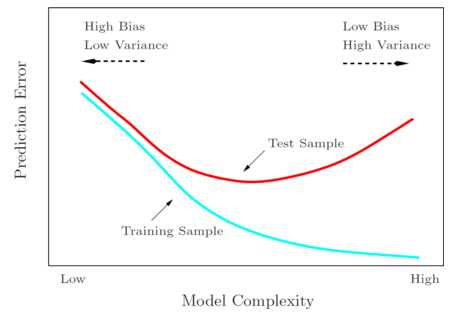
- 经验风险最小化中，
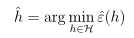这个得到的函数具有最小的训练误差，但是如上图所示，并不具有最小的一般误差。
2、无限假设类情形
- VC维：只要存在大小为d的集合可以被某个假设空间分散，那么这个假设的VC维就是d。
在经验风险最小化中，最终的目的就是确定模型所需样本数的界限，这个界限是宽松的，这也是为什么在界限的表达时通常使用O这个符号来表示的原因。此外，这个界限对于符合任何分布的数据均成立，即使在最坏的情形下也是成立。但是在实际应用中，无法直接通过这个界限来确定我们所需的样本数量，因为在实际问题中，我们所研究的某个问题往往服从特定的分布，并不像最坏的情形那样糟糕，若直接将参数代入求解m的界，往往会得到非常大的m的值。
三、模型选择
1、保留交叉验证法
- 通常只利用了70％左右的数据，造成了浪费
2、K折交叉验证法
- 每个模型都需要训练K次，需要大量的计算
3、留一交叉验证法
- m = k,即每次只留下一个样本作为测试数据
- 能够更充分得利用数据，但是计算量更大
- 当数据非常少时才适用
四、特征选择
1、前向查找和反向查找
- 这两种算法是一种启发式搜索算法，并不保证一定能找到最优的特征集。
- 在文本分类问题中，特征向量往往非常大，一般是几万的量级，此时选用这两种算法不大合适，因为所需要的计算量太大了。
2、过滤特征选择
- 通过计算为每个特征向量$x_{i}$计算其对结果y的贡献值，然后选择贡献值最大的k个特征。
- 如何决定k取多少？一个方法是通过交叉验证，不停选择前一个特征、前两个特征、前三个特征等等，以此来决定要选择几个特征值。
五、贝叶斯统计和规则化
- 频率派：将参数$\theta$视为未知的常量，并采用最大似然估计法去求解。
- 贝叶斯学派：将参数$\theta$视为未知的随机变量。
- 贝叶斯统计和规则化，就是找出新的估计方法来代替原有的最大似然估计法，来减少过拟合的发生。
