------------------------------------------------------
这是蒟蒻对CRT的一些见解
如有错误欢迎指出,不胜感激
长话短说
对于一组同余方程
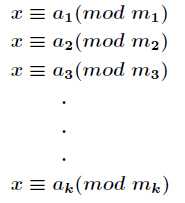
如果保证$ m_1$, $ m_2$ ... $ m_k$ 两两互质, 且令P为 $ m_1$, $ m_2$ ... $ m_k$ 之积
则有结论 x ≡ ($ a_1$$ M_1$$ M_1^{-1}$ + $ a_2$$ M_2$$ M_2^{-1}$ + ... + $ a_k$$ M_k$$ M_k^{-1}$)(mod P)
其中 $ M_i$为$ \frac{P}{ m_i}$,$ M_i^{-1}$为$ M_i$在模$ m_i$意义下的逆元($ M_i$$ M_i^{-1}$≡1(mod $ m_i$))
证明:
∵ $ m_1$, $ m_2$ ... $ m_k$两两互质
∴ $ M_i$ 在模$ m_i$意义下一定存在逆元($ M_i$与$ m_i$ 互质)
那么对于第i个方程 x≡$a_i $(mod $ m_i$)
由于对于任何的k≠i,有$ m_i|M_k$ , 因而会影响余数的只有$ a_iM_iM_i^{-1}$ 一项
又∵$ M_i$$ M_i^{-1}$在模$ m_i$意义下等于1,因而结论正确
