https://zybuluo.com/ysner/note/1099145
标签(空格分隔): 主席树
前置技能
- 线段树
- 动态开点
- 标记永久化
离散化
定义
主席树=可持久化线段树=函数式线段树
线段树经过了若干次修改之后,仍然能找到原来某次修改前的线段树的信息的一种数据结构建立
据说最无脑的方法是每修改一次新建一颗主席树???
单点修改:
- 线段树单点修改只会改变\(log\)个点(一条链),主席树同理。
- 那为什么要新建一颗主席树呢?新建修改过的链,再同原来的点接起来,这效果不是一样的吗?
区间修改:
- 如果像单点修改一样新建修改过的点,显然不好也不能\(Pushdown\)
- 这个问题可以用标记永久化解决
使用
1、静态整体Kth
滑稽吧...sort一遍就好了。
时间复杂度\(O(nlogn)\) 空间复杂度\(O(n)\)
2、动态整体Kth
离散化后开一棵权值线段树,每个位置的值表示这个位置对应的那个数(离散化后的)有多少个,向上维护和;
查询时先查询左子树和sum,比较k和sum的大小:若k<=sum则说明第k小数在左子树中,递归查询左子树;
否则,这个数对应的就是右子树中第k-sum小的数,k-=sum,递归查询右子树。
时间复杂度\(O(nlogn)\) 空间复杂度\(O(n)\)
3、静态区间Kth
对每个点以其前缀开一棵权值线段树,那么任意一段区间均可以表示成为两棵权值线段树作差,即R位置的线段树减去L-1位置上的线段树
每个点开一棵线段树空间复杂度\(O(n^2)\),MLE,考虑到后一个位置相比于前一个位置的更改只有\(logn\)个节点,所以使用主席树
时间复杂度\(O(nlogn)\) 空间复杂度\(O(nlogn)\)
4、动态区间Kth (不会实现!!!)
还是要想办法维护前缀和。如果只是同3、的前缀和的话,就要对前缀和进行\(O(nlogn)\)的单次修改,显然TLE。
这里考虑用树状数组维护前缀和。修改时,可以只修改logn个位置,复杂度\(O(log^2n)\);
查询时,依旧是R位置减去L-1位置,这时候不再是两棵线段树作差,而是log棵线段树与log棵线段树作差;跳的时候,log个节点一起跳到左子树/右子树
时间复杂度\(O(nlog^2n)\) 空间复杂度\(O(nlog^2n)\)
例题
T1
Luogu3834 【模板】可持久化线段树 1(主席树)
求静态区间第K小查询区间[l,r]第k小?
可以开一棵值域线段树,维护数的个数
把数字离散化之后丢进线段树中去
然后直接在线段树上二分数字
如果k大于当前点左子树的点的个数,那么k减去这个个数,去右子树
否则去左子树
已知第i棵线段树保存前i个数字
那么运用前缀和的方法,把第r棵线段树和第l?1棵线段树作差,得到的就是这个区间内的数。
T2
Luogu3567 [POI2014]KUR-Couriers
每次询问一个区间内有没有一个数出现次数超过一半一个区间内只会有一个数满足要求
主席树维护数的个数(即sort+unqiue+lower_bound)
L?1和R值域线段树做差,直接树上二分查询
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define re register
#define il inline
#define lson t[x].ls
#define rson t[x].rs
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int N=5e5+100;
int tot,L,R,rt[N],n,m;
struct seg{int ls,rs,num;}t[N*30];
il int gi()
{
re int x=0,t=1;
re char ch=getchar();
while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar();
if(ch==‘-‘) t=-1,ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar();
return x*t;
}
il void Build(re int &x,re int l,re int r)
{
x=++tot;
if(l>=r) return;
re int mid=l+r>>1;
Build(lson,l,mid);Build(rson,mid+1,r);
}
il void Modify(re int &x,re int l,re int r,re int pos)
{
t[++tot]=t[x];t[x=tot].num++;
if(l>=r) return;
re int mid=l+r>>1;
if(pos<=mid) Modify(lson,l,mid,pos);
else Modify(rson,mid+1,r,pos);
}
il int Query(re int A,re int B,re int l,re int r)
{
if(l>=r) return l;
re int mx=max(t[t[B].ls].num-t[t[A].ls].num,t[t[B].rs].num-t[t[A].rs].num);
if(mx*2<=(R-L+1)) return 0;
re int mid=l+r>>1;
if(t[t[B].ls].num-t[t[A].ls].num==mx) return Query(t[A].ls,t[B].ls,l,mid);
else return Query(t[A].rs,t[B].rs,mid+1,r);
}
int main()
{
n=gi();m=gi();
Build(rt[0],1,n);
fp(i,1,n)
{
re int x=gi();rt[i]=rt[i-1];
Modify(rt[i],1,n,x);
}
while(m--)
{
L=gi(),R=gi();
printf("%d\n",Query(rt[L-1],rt[R],1,n));
}
return 0;
}T3
Luogu3168 [CQOI2015]任务查询系统
有m个有优先级的任务,在时间区间[l,r]内被计算机运行
n个询问,求第x秒正在运行的前k小的任务优先级之和把一个任务拆成两个,在l秒时加入,在r+1时减去
然后每个时间开值域的主席树就好了
// luogu-judger-enable-o2
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define re register
#define il inline
#define lson t[x].ls
#define rson t[x].rs
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int N=1e5+100;
int tot,L,R,rt[N],id[N],len,ans=1,n,m;
struct seg{int ls,rs,num,sum;}t[N*50];
struct tas
{
int t,w,f;
bool operator < (const tas &o) const {return t<o.t;}
}a[N<<1];
il int gi()
{
re int x=0,t=1;
re char ch=getchar();
while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar();
if(ch==‘-‘) t=-1,ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar();
return x*t;
}
il void Modify(re int &x,re int l,re int r,re int pos,re int k)
{
t[++tot]=t[x];x=tot;
t[x].num+=k;t[x].sum+=k*id[pos];
if(l>=r) return;
re int mid=l+r>>1;
if(pos<=mid) Modify(lson,l,mid,pos,k);
else Modify(rson,mid+1,r,pos,k);
}
il ll Query(re int x,re int l,re int r,re int k)
{
if(l>=r) return t[x].num?(1ll*t[x].sum/t[x].num*k):0;
re int mid=l+r>>1;
if(k<=t[lson].num) return Query(lson,l,mid,k);
else return t[lson].sum+Query(rson,mid+1,r,k-t[lson].num);
}
int main()
{
m=gi();n=gi();
fp(i,1,m)
{
re int s=gi(),e=gi(),f=gi();
a[i*2-1]=(tas){s,f,1};a[i*2]=(tas){e+1,f,-1};id[i]=f;
}
sort(a+1,a+2*m+1);sort(id+1,id+1+m);
len=unique(id+1,id+1+m)-id-1;
for(re int i=1,j=1;i<=n;i++)
{
rt[i]=rt[i-1];
for(;a[j].t==i;j++)
{
re int x=lower_bound(id+1,id+1+len,a[j].w)-id;
Modify(rt[i],1,len,x,a[j].f);
}
}
fp(i,1,n)
{
re int X=gi(),A=gi(),B=gi(),C=gi(),Y;
Y=(1ll*A*ans+B)%C+1;ans=Query(rt[X],1,len,Y);
printf("%lld\n",ans);
}
return 0;
}T4
Luogu2839 [国家集训队]middle
求左端点在[a,b]之间,右端点在[c,d]之间的序列中,最大的中位数。考虑二分答案
Check把小于它的设为?1,大于等于它的设为1
维护三个玩意儿
[a,b]求一个最大后缀子段和
[c,d]求一个最大前缀子段和
[b+1,c?1]求一个和
加起来如果大于等于0,那么满足要求,即这个数还可以变大,否则就只能缩小
每个数开一个线段树来做,空间开不下,用主席树即可
Update:
- get一个新姿势“线段树返回结构体???
RE不止是因为空间开炸了???
// luogu-judger-enable-o2 #include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #define lson t[x].ls #define rson t[x].rs #define re register #define il inline #define ll long long #define fp(i,a,b) for(re int i=a;i<=b;i++) #define fq(i,a,b) for(re int i=a;i>=b;i--) using namespace std; const int N=5e5+100; struct seg{int sum,ls,rs,lm,rm;}t[N*10]; struct ppl { int id,d; bool operator < (const ppl &o) const {return d<o.d;} }num[N]; struct Res{int sum,ls,rs,lm,rm;}r[N*10]; int n,Q,ans,q[10],a[N],len,A,B,C,D,tot,rt[N]; il int gi() { re int x=0,t=1; re char ch=getchar(); while(ch!=‘-‘&&(ch<‘0‘||ch>‘9‘)) ch=getchar(); if(ch==‘-‘) t=-1,ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar(); return x*t; } il void Update(re int x) { t[x].lm=max(t[lson].lm,t[lson].sum+t[rson].lm); t[x].rm=max(t[rson].rm,t[lson].rm+t[rson].sum); t[x].sum=t[lson].sum+t[rson].sum; } il void Build(re int &x,re int l,re int r) { x=++tot; if(l==r) {t[x].sum=t[x].lm=t[x].rm=1;return;} re int mid=l+r>>1; Build(lson,l,mid);Build(rson,mid+1,r); Update(x); } il void Modify(re int &x,re int l,re int r,re int pos) { t[++tot]=t[x];x=tot; if(l==r) {t[x].sum=t[x].lm=t[x].rm=-1;return;} re int mid=l+r>>1; if(pos<=mid) Modify(lson,l,mid,pos);else if(pos>mid)Modify(rson,mid+1,r,pos); Update(x); } il Res Merge(Res x,Res y) { Res z; z.sum=x.sum+y.sum; z.lm=max(x.lm,y.lm+x.sum); z.rm=max(y.rm,y.sum+x.rm); return z; } il Res Query(re int x,re int l,re int r,re int ql,re int qr) { if(ql<=l&&r<=qr) { re Res tmp=(Res){t[x].sum,0,0,t[x].lm,t[x].rm}; return tmp; } re int mid=l+r>>1; if(qr<=mid) return Query(lson,l,mid,ql,qr); else if(ql>mid) return Query(rson,mid+1,r,ql,qr); else return Merge(Query(lson,l,mid,ql,qr),Query(rson,mid+1,r,ql,qr)); } il void wri(re int x) { if(x<0) putchar(‘-‘),x=-x; if(x>9) wri(x/10); putchar(x%10+48); } int main() { n=gi();fp(i,1,n) a[i]=num[i].d=gi(),num[i].id=i; sort(a+1,a+1+n); len=unique(a+1,a+1+n)-a-1; fp(i,1,n) num[i].d=lower_bound(a+1,a+1+len,num[i].d)-a; sort(num+1,num+1+n); Q=gi(); Build(rt[1],1,n); fp(i,2,n) { rt[i]=rt[i-1]; Modify(rt[i],1,n,num[i-1].id); } while(Q--) { A=gi();B=gi();C=gi();D=gi(); q[0]=(A+ans)%n+1,q[1]=(B+ans)%n+1,q[2]=(C+ans)%n+1,q[3]=(D+ans)%n+1; sort(q,q+4);A=q[0],B=q[1],C=q[2],D=q[3]; re int res=0,dat,l=1,r=n; while(l<=r) { re int mid=l+r>>1; if(B+1<=C-1) dat=Query(rt[mid],1,n,B+1,C-1).sum; else dat=0; dat+=Query(rt[mid],1,n,A,B).rm+Query(rt[mid],1,n,C,D).lm; if(dat>=0) res=num[mid].d,l=mid+1; else r=mid-1; } ans=a[res]; wri(ans);puts(""); } return 0; }
T5
Luogu2633 Count on a tree
问u和v这两个节点间第K小的点权。主席树还是为值域线段树,维护数的个数(开w和o两个数组就成了,x无必要)
每个点的线段树版本由它的父亲加入它的点权得到
那么每个点的线段树存的就是它到根的所有点的点权
还是树上二分数字,还是线段树作差:
用rt[i]表示i这个点的线段树
那么就是这样作差rt[u]+rt[v]?rt[lca]?rt[fa[lca]]
这样就只包含了u,v路径上所有的点了
// luogu-judger-enable-o2
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define re register
#define il inline
#define lson t[x].ls
#define rson t[x].rs
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int N=1e5+100;
int n,m,o[N],h[N],cnt,w[N],x[N],len,tot,tim,sz[N],son[N],f[N],d[N],ans,rt[N],top[N];
struct Edge{int to,next;}e[N<<1];
struct seg{int ls,rs,num;}t[N*30];
il void add(re int u,re int v){e[++cnt]=(Edge){v,h[u]};h[u]=cnt;}
il int gi()
{
re int x=0,t=1;
re char ch=getchar();
while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar();
if(ch==‘-‘) t=-1,ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar();
return x*t;
}
il void wri(re int x)
{
if(x<0) putchar(‘-‘),x=-x;
if(x>9) wri(x/10);
putchar(x%10+‘0‘);
}
il void Build(re int &x,re int l,re int r)
{
x=++tot;
if(l==r) return;
re int mid=l+r>>1;
Build(lson,l,mid);Build(rson,mid+1,r);
}
il void Modify(re int &x,re int fa,re int l,re int r,re int pos)
{
t[x=++tot]=t[fa];t[x].num++;
if(l==r) return;
re int mid=l+r>>1;
if(pos<=mid) Modify(lson,t[fa].ls,l,mid,pos);else Modify(rson,t[fa].rs,mid+1,r,pos);
}
il void dfs1(re int u,re int fa,re int deep)
{
sz[u]=1;f[u]=fa;d[u]=deep;
Modify(rt[u],rt[fa],1,len,x[u]);
for(re int i=h[u];i+1;i=e[i].next)
{
re int v=e[i].to;
if(v==fa) continue;
dfs1(v,u,deep+1);
sz[u]+=sz[v];
if(sz[son[u]]<sz[v]) son[u]=v;
}
}
il void dfs2(re int u,re int up)
{
top[u]=up;
if(son[u]) dfs2(son[u],up);
for(re int i=h[u];i+1;i=e[i].next)
{
re int v=e[i].to;
if(v==f[u]||v==son[u]) continue;
dfs2(v,v);
}
}
il int get_lca(re int u,re int v)
{
while(top[u]^top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=f[top[u]];
}
if(d[u]>d[v]) swap(u,v);
return u;
}
il int Query(re int A,re int B,re int C,re int D,re int l,re int r,re int k)
{
if(l==r) return l;
re int tmp=t[t[A].ls].num+t[t[B].ls].num-t[t[C].ls].num-t[t[D].ls].num,mid=l+r>>1;
if(k<=tmp) return Query(t[A].ls,t[B].ls,t[C].ls,t[D].ls,l,mid,k);else return Query(t[A].rs,t[B].rs,t[C].rs,t[D].rs,mid+1,r,k-tmp);//swap(k,tmp)???!!!!!
}
int main()
{
memset(h,-1,sizeof(h));
n=gi();m=gi();
fp(i,1,n) o[i]=w[i]=gi();sort(o+1,o+1+n);///where is sort???
len=unique(o+1,o+1+n)-o-1;
fp(i,1,n) x[i]=lower_bound(o+1,o+1+len,w[i])-o;///why the last letter is x???
fp(i,1,n-1)
{
re int u=gi(),v=gi();
add(u,v);add(v,u);
}
Build(rt[0],1,len);
dfs1(1,0,1);dfs2(1,1);
while(m--)
{
re int u=gi()^ans,v=gi(),lca=get_lca(u,v),k=gi();
ans=o[Query(rt[u],rt[v],rt[lca],rt[f[lca]],1,len,k)];
wri(ans);puts("");
}
return 0;
}T6
Luogu3302 [SDOI2013]森林
1.询问x-y这条链上点权的第k小。保证x,y在同一个连通块里。
2.连接x,y两点。保证x,y在不同的连通块里。
操作一和count on a tree一样,现在考虑操作二怎么处理。
题目中多次提到联通块,这意味者什么?
意味着加边过程实际上是联通块合并的过程。
我们可以先dfs遍历所有点,给每个点标上其所属的联通块。
当连边时,我们把联通块合并(当然要用启发式合并啦),让大的联通块吞并小的联通块时,我们要改变每个点的所属,改变它的父亲,改边点的层数,改变联通块的大小(就是链剖一开始维护的东西)。
但总不能重新链剖吧?
于是只能用倍增求lca,这样dfs时改变一个点的父亲后就可以更新倍增数组。
Update:
空间一定要多开,保险1e7???
#include<iostream> #include<cmath> #include<cstring> #include<cstdio> #include<cstdlib> #include<algorithm> #define ll long long #define re register #define il inline #define lson t[x].ls #define rson t[x].rs #define fp(i,a,b) for(re int i=a;i<=b;i++) #define fq(i,a,b) for(re int i=a;i>=b;i--) using namespace std; const int N=5e5+100; int n,m,T,o[N],w[N],h[N],cnt,len,f[N][20],d[N],sz[N],ff[N],tot,rt[N],ans; bool vis[N]; char s[10]; struct Edge{int to,next;}e[N<<1]; struct seg{int ls,rs,num;}t[N*20]; il void add(re int u,re int v){e[++cnt]=(Edge){v,h[u]};h[u]=cnt;} il int gi() { re int x=0,t=1; re char ch=getchar(); while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar(); if(ch==‘-‘) t=-1,ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar(); return x*t; } il void wri(re int x) { if(x<0) putchar(‘-‘),x=-x; if(x>9) wri(x/10); putchar(x%10+‘0‘); } il void Modify(re int &x,re int fa,re int l,re int r,re int pos) { t[x=++tot]=t[fa];t[x].num++; if(l==r) return; re int mid=l+r>>1; if(pos<=mid) Modify(lson,t[fa].ls,l,mid,pos);else Modify(rson,t[fa].rs,mid+1,r,pos); } il void dfs(re int u,re int fa,re int st) { d[u]=d[fa]+1;vis[u]=1;f[u][0]=fa;sz[st]++;ff[u]=st; fp(i,1,16) f[u][i]=f[f[u][i-1]][i-1]; Modify(rt[u],rt[f[u][0]],1,len,w[u]); for(re int i=h[u];i+1;i=e[i].next) { re int v=e[i].to; if(v==fa) continue; dfs(v,u,st); } } il void Build(re int &x,re int l,re int r) { x=++tot; if(l==r) return; re int mid=l+r>>1; Build(lson,l,mid);Build(rson,mid+1,r); } il int get_lca(re int u,re int v) { if(d[u]<d[v]) swap(u,v); fq(i,16,0) if(d[u]-(1<<i)>=d[v]) u=f[u][i]; if(u==v) return u; fq(i,16,0) if(f[u][i]^f[v][i]) u=f[u][i],v=f[v][i]; return f[u][0]; } il int Query(re int A,re int B,re int C,re int D,re int l,re int r,re int k) { if(l==r) return l; re int tmp=t[t[A].ls].num+t[t[B].ls].num-t[t[C].ls].num-t[t[D].ls].num,mid=l+r>>1; if(k<=tmp) return Query(t[A].ls,t[B].ls,t[C].ls,t[D].ls,l,mid,k);else return Query(t[A].rs,t[B].rs,t[C].rs,t[D].rs,mid+1,r,k-tmp); } int main() { memset(h,-1,sizeof(h)); gi();n=gi();m=gi();T=gi(); fp(i,1,n) o[i]=w[i]=gi(),ff[i]=i;///ff要初始值 sort(o+1,o+1+n); len=unique(o+1,o+1+n)-o-1; fp(i,1,n) w[i]=lower_bound(o+1,o+1+len,w[i])-o; fp(i,1,m) { re int u=gi(),v=gi(); add(u,v);add(v,u); } Build(rt[0],1,len); fp(i,1,n) if(!vis[i]) dfs(i,0,i); while(T--) { scanf("%s",s); if(s[0]==‘Q‘) { re int u=gi()^ans,v=gi()^ans,lca=get_lca(u,v),k=gi()^ans; ans=o[Query(rt[u],rt[v],rt[lca],rt[f[lca][0]],1,len,k)]; wri(ans),puts(""); } else { re int u=gi()^ans,v=gi()^ans; if(sz[ff[u]]<sz[ff[v]]) swap(u,v); dfs(v,u,ff[u]); add(u,v);add(v,u); } } return 0; }T8
Luogu3293 [SCOI2016]美味
一家餐厅有 n 道菜,编号 1...n ,大家对第 i 道菜的评价值为 \(a_i\)(1<=i<=n)。有 m 位顾客,第 i 位顾客的期望值为 \(b_i\),而他的偏好值为 \(x_i\) 。因此,第 i位顾客认为第j 道菜的美味度为\(b_i\bigotimes(a_j+x_i)\).他只能从第 \(l_i\) 道到第 \(r_i\) 道中选择。请你帮助他们找出最美味的菜。
二分\(a_j+x_i\)
针对\(b_i\)从大到小枚举位数,尽可能使大位为1.
这一位填1或0显然都可以缩小答案范围,于是在这个范围内查找看是否存在\(mid-x_i\)这一数即可。显然可以主席树维护。
Update:注意一下边界
// luogu-judger-enable-o2
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define re register
#define il inline
#define lson t[x].ls
#define rson t[x].rs
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int N=5e5+100,len=1e5;
int n,m,w[N],tot,rt[N],b,l,x,r,ans,f,sz[N];
struct seg{int ls,rs,sz;}t[N*10];
il int gi()
{
re int x=0,t=1;
re char ch=getchar();
while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar();
if(ch==‘-‘) t=-1,ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar();
return x*t;
}
il void wri(re int x)
{
if(x<0) putchar(‘-‘),x=-x;
if(x>9) wri(x/10);
putchar(x%10+‘0‘);
}
il void Build(re int &x,re int l,re int r)
{
x=++tot;
if(l==r) return;
re int mid=l+r>>1;
Build(lson,l,mid);Build(rson,mid+1,r);
}
il void Modify(re int &x,re int l,re int r,re int pos)
{
t[++tot]=t[x];++t[x=tot].sz;
if(l==r) return;
re int mid=l+r>>1;
if(pos<=mid) Modify(lson,l,mid,pos);else Modify(rson,mid+1,r,pos);
}
il int Query(re int A,re int B,re int l,re int r,re int ql,re int qr)
{
if(ql<=l&&r<=qr) return t[B].sz-t[A].sz;
re int mid=l+r>>1,res=0;
if(ql<=mid) res=Query(t[A].ls,t[B].ls,l,mid,ql,qr);
if(qr>mid) res+=Query(t[A].rs,t[B].rs,mid+1,r,ql,qr);
return res;
}
int main()
{
n=gi();m=gi();
Build(rt[0],1,len);
fp(i,1,n) w[i]=gi(),rt[i]=rt[i-1],Modify(rt[i],0,len,w[i]);//数据范围这么小,连离散化都不需要。。。
while(m--)
{
ans=0;
b=gi(),x=gi(),l=gi(),r=gi();re int L,R;
fq(j,17,0)//别忘了处理最后一位
{
if((1<<j)&b) L=ans,R=ans+(1<<j)-1,f=0;//该位填0
else L=ans+(1<<j),R=ans+(1<<j+1)-1,f=1;//该位填1
if(!Query(rt[r],rt[l-1],0,len,max(0,L-x),min(R-x,len))) f^=1;//没这数
ans|=(f<<j);
}
wri(ans^b);puts("");
}
return 0;
}T9
Luogu2468 [SDOI2010]粟粟的书架
[题面戳我][https://www.luogu.org/problemnew/show/P2468]
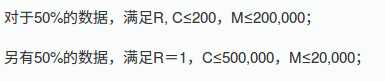
吐槽一句,强行二合一有意思不???
- 二维的50分,开数组\(sum[i][j][k]\),\(gs[i][j][k]\)分别记录左上点为\((1,1)\),右下点为\((i,j)\)的矩阵中大于等于\(k\)的数的和 和 个数。二分k即可。
一维的50分,开主席树维护页数,每次在主席树里找出足够大的和。(???)
Update:二维那里,二分完后可能有多余的个数。why?#include<iostream> #include<cmath> #include<cstring> #include<cstdio> #include<cstdlib> #include<algorithm> #define ll long long #define re register #define il inline #define lson t[x].ls #define rson t[x].rs #define fp(i,a,b) for(re int i=a;i<=b;i++) #define fq(i,a,b) for(re int i=a;i>=b;i--) using namespace std; const int N=1050,len=1000; int r,c,m,a,gs[210][210][1010],sum[210][210][1010],sm[500005],tot,rt[500005],L,R,h,ans; struct seg{int ls,rs,sz,sum;}t[10000000]; il int gi() { re int x=0,t=1; re char ch=getchar(); while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar(); if(ch==‘-‘) t=-1,ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar(); return x*t; } il void wri(re int x) { if(x<0) putchar(‘-‘),x=-x; if(x>9) wri(x/10); putchar(x%10+‘0‘); } il void Modify(re int &x,re int l,re int r,re int pos) { t[++tot]=t[x];++t[x=tot].sz;t[x].sum+=pos; if(l==r) return; re int mid=l+r>>1; if(pos<=mid) Modify(lson,l,mid,pos);else Modify(rson,mid+1,r,pos); } il int Query(re int A,re int B,re int l,re int r) { if(l==r) return (h+l-1)/l; re int mid=l+r>>1,tmp=t[t[A].rs].sum-t[t[B].rs].sum; if(tmp>=h) return Query(t[A].rs,t[B].rs,mid+1,r); else {h-=tmp;return t[t[A].rs].sz-t[t[B].rs].sz+Query(t[A].ls,t[B].ls,l,mid);} } int main() { r=gi();c=gi();m=gi(); if(r>1) { fp(i,1,r) fp(j,1,c) { re int x=gi(); fp(k,1,1000) { sum[i][j][k]=sum[i-1][j][k]+sum[i][j-1][k]-sum[i-1][j-1][k]; gs[i][j][k]=gs[i-1][j][k]+gs[i][j-1][k]-gs[i-1][j-1][k]; if(x>=k) sum[i][j][k]+=x,gs[i][j][k]++; } } while(m--) { re int l=1,r=1000,ans=1001,x=gi(),y=gi(),xx=gi(),yy=gi(),h=gi(); while(l<=r) { re int mid=l+r>>1; if(sum[xx][yy][mid]-sum[x-1][yy][mid]-sum[xx][y-1][mid]+sum[x-1][y-1][mid]>=h) ans=mid,l=mid+1; else r=mid-1; } if(ans==1001) {puts("Poor QLW");continue;} re int ans1=gs[xx][yy][ans]-gs[x-1][yy][ans]-gs[xx][y-1][ans]+gs[x-1][y-1][ans],ans2=sum[xx][yy][ans]-sum[x-1][yy][ans]-sum[xx][y-1][ans]+sum[x-1][y-1][ans]-h; wri(ans1-ans2/ans);puts(""); } } else { fp(i,1,c) a=gi(),rt[i]=rt[i-1],Modify(rt[i],1,1000,a); while(m--) { gi();L=gi();gi();R=gi();h=gi(); if(t[rt[R]].sum-t[rt[L-1]].sum<h) {puts("Poor QLW");continue;} else printf("%d\n",Query(rt[R],rt[L-1],1,1000)); } } return 0; }T10
Luogu2048 [NOI2010]超级钢琴
求给定序列中长度为L~R之间的前k大子序列的和
有一个很暴力的想法,就是把所有合法的状态丢到一个堆里面,然后依次取出最大值。这样的话时间是\(O(n^2logn)\),空间是\(O(n^2)\).
我们考虑优化这个过程。对于右端点相同的所有合法区间,我们只在堆中保留最大的一个,在取出这一个以后再丢入次大的,取出次大的再丢入次次大的,以此类推。这样可以保证正确性,同时空间被优化到了\(O(n)\)
现在我们考虑怎么查这个次次次次(这里有若干个次)大值。
首先把区间和转化成前缀和相减,因为我们固定了右端点,那么最大值就是对应了前缀和中减去的那个值最小。而第k大值刚好对应减去的那个数第k小,同时还要保证在一定区间范围内(L、R的限制)。所以离散前缀和以后主席树即可。
注意前缀和减去的部分可以是0,所以0也要被离散进去。// luogu-judger-enable-o2 #include<iostream> #include<cmath> #include<cstring> #include<cstdio> #include<cstdlib> #include<algorithm> #include<queue> #define ll long long #define re register #define il inline #define lson t[x].ls #define rson t[x].rs #define fp(i,a,b) for(re int i=a;i<=b;i++) #define fq(i,a,b) for(re int i=a;i>=b;i--) using namespace std; const int N=1e6+100; struct seg{int ls,rs,num;}t[N*10]; struct node { int x,k;ll w; bool operator < (const node &o) const {return w<o.w;} }; priority_queue<node>Q; int n,k,L,R,w[N],o[N],len,tot,rt[N]; ll ans; il int gi() { re int x=0,t=1; re char ch=getchar(); while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar(); if(ch==‘-‘) t=-1,ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-48,ch=getchar(); return x*t; } il void Modify(re int &x,re int l,re int r,re int pos) { t[++tot]=t[x];t[x=tot].num++; if(l==r) return; re int mid=l+r>>1; if(pos<=mid) Modify(lson,l,mid,pos);else Modify(rson,mid+1,r,pos); } il int Query(re int A,re int B,re int l,re int r,re int k) { if(l==r) return l; re int mid=l+r>>1,tmp=t[t[A].ls].num-t[t[B].ls].num; if(k<=tmp) return Query(t[A].ls,t[B].ls,l,mid,k); else return Query(t[A].rs,t[B].rs,mid+1,r,k-tmp); } int main() { n=gi();k=gi();L=gi();R=gi();++n; fp(i,2,n) o[i]=w[i]=gi()+w[i-1]; sort(o+1,o+1+n); len=unique(o+1,o+1+n)-o-1; fp(i,1,n) w[i]=lower_bound(o+1,o+1+len,w[i])-o; fp(i,1,n) rt[i]=rt[i-1],Modify(rt[i],1,len,w[i]); fp(i,L+1,n) Q.push((node){i,1,o[w[i]]-o[Query(rt[i-L],rt[max(0,i-R-1)],1,len,1)]}); while(k--) { node tmp=Q.top();Q.pop(); ans+=tmp.w; if(tmp.k==min(R-L+1,tmp.x-L)) continue; tmp.k++; tmp.w=o[w[tmp.x]]-o[Query(rt[tmp.x-L],rt[max(0,tmp.x-R-1)],1,len,tmp.k)]; Q.push(tmp); } printf("%lld\n",ans); return 0; }
