大整数求和
摘要:对于一些大整数,如果超出电脑整型数所能表示的最大范围,应该怎么计算加法呢?我们可以利用字符串进行求和,具体代码如下:
1 #include<iostream> 2 #include<string> 3 using namespace std; 4 string Add(string &str1, string &str2); 5 int main() 6 { 7 string str1, str2; 8 cin >> str1 >> str2; 9 cout << Add(str1, str2) << endl; 10 } 11 12 string Add(string & str1, string & str2) 13 { 14 int flag = 0; // 进位标记 15 int i = 0; // 位数 16 int n = str1.size(); 17 int m = str2.size(); 18 // 整数是从最低位开始相加,所以先将字符串反序 19 reverse(str1.begin(), str1.end()); 20 reverse(str2.begin(), str2.end()); 21 string res = "";// 存放结果的串 22 while (i < n && i < m) 23 { 24 res+=(((str1[i] - ‘0‘) + (str2[i] - ‘0‘) + flag) % 10 + ‘0‘);// 计算第i位的值 25 flag = ((str1[i] - ‘0‘) + (str2[i] - ‘0‘) + flag) / 10; // 计算第i位的进位 26 i++; 27 } 28 // 如果str1表示的整数位数更多,计算大整数str1余下的部分 29 while (i < n) 30 { 31 res+= (((str1[i] - ‘0‘) + flag) % 10 + ‘0‘);// 计算第i位的值 32 flag = ((str1[i] - ‘0‘) + flag) / 10; // 计算第i位的进位 33 i++; 34 } 35 // 如果str2表示的整数位数更多,计算大整数str2余下的部分 36 while (i < m) 37 { 38 res+= (((str2[i] - ‘0‘) + flag) % 10 + ‘0‘);// 计算第i位的值 39 flag = ((str2[i] - ‘0‘) + flag) / 10; // 计算第i位的进位 40 i++; 41 } 42 // 最高位是否有进位,设置最高位的值 43 int d = (n > m) ? n : m; 44 if (flag == 1) 45 res+= ‘1‘; 46 // 反序结果串,结果即为所求 47 reverse(res.begin(), res.end()); 48 return res; 49 }
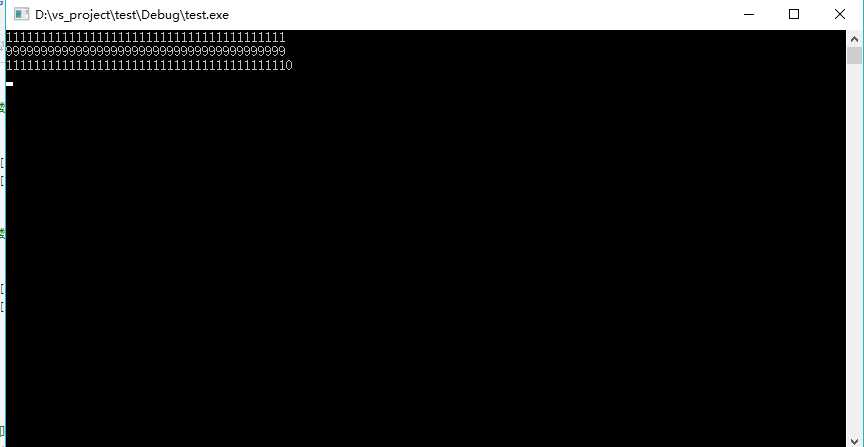
运行结果如下: