Prufer序列
这个很全啊,看这吧。
不写了。
主要参考洛谷课件。其实是没时间了懒得找
\(Defination\)
Prufer序列是一种无根树的编码表示。
对于一棵\(n\)个点的无根树,对应唯一一串长度为\(n-2\)的\(Prufer\)序列。
无根树转\(Prufer\)序列
定义无根树中度数为\(1\)的节点是叶子节点,每次找到编号最小的叶节点删除,在序列中添加与之相邻的点。如此重复直到剩下最后两个节点。
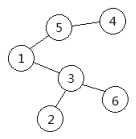
上图对应无根树的\(Prufer\)序列为\(3,5,1,3\)。
\(Prufer\)序列转有根树
给定点集\(G={1,2,\ldots,n}\),\(Prufer\)序列\([a_1,a_2,\ldots,a_{n-2}]\)。
每次取出\(Prufer\)序列中的第一个元素\(x_i\),在\(G\)中找在当前\(Prufer\)序列中没有出现的第一个元素\(y_i\),在\(x_i\)和\(y_i\)间连一条边;将\(x_i\)从\(Prufer\)序列中删除,\(y_i\)从\(G\)中删除。
最后\(G\)中还剩下\(2\)个元素,在这\(2\)个元素间连一条边。
