二叉树的定义

类型名称：二叉树

数据对象集：一个有穷的结点集合。若不为空，则有根结点和其左、右二叉子树组成。

操作集：BT∈BinTree, Item∈ElementType，重要操作有：

1、Boolean IsEmpty（BinTree BT）：判别BT是否为空

2、void Traversal（BinTree BT）：遍历，按某顺序访问每个结点

3、BinTree CreateBinTree（）：创建一个二叉树

常用的遍历方法有：

void PreOrderTraversal（BinTree BT）：先序----根、左子树、右子树

void InOrderTraversal（BinTree BT）：中序----左子树、根、右子树

void PostOrderTraversal（BinTree BT）：后序---左子树、右子树、根

void LevelOrderTraversal（BinTree BT）：层次遍历，从上到下、从左到右

二叉树的遍历

（1）先序遍历

遍历过程为：

①访问根结点；

②先序遍历其左子树；

③先序遍历其右子树。

void PreOrderTraversal(BinTree BT)
{
    if(BT) {
        printf("%d", BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

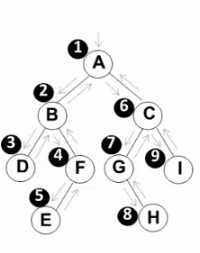
（2）中序遍历

遍历过程为：

①中序遍历其左子树；

②访问根结点；

③中序遍历其右字树。

void InOrderTraversal(BinTree BT)
{
    if(BT) {
        InOrderTraversal(BT->Left);
        printf("%d", BT->Data);
        InOrderTraversal(BT->Right);
    }
}

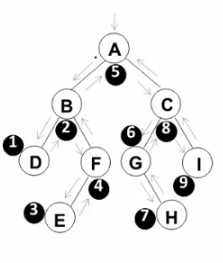
（3）后序遍历

遍历过程为：

①后序遍历其左子树

②后序遍历其右子树

③访问根结点

void PostOrderTraversal(BinTree BT)
{
    if(BT) {
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        printf("%d", BT->Data);
    }
}

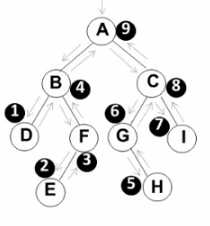
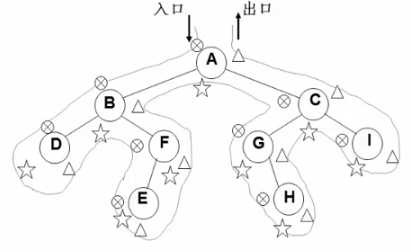
先序、中序、后序遍历过程：遍历过程中经过结点的路线一样，只是各结点的时机不同。

图中在从入口到出口的曲线上用三种符号分别标记了先序、中序和后序访问各结点的时刻。