
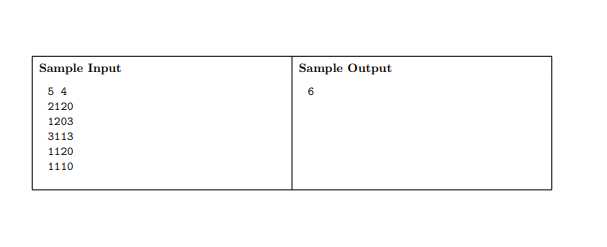
题意:
从左上角跳到右下角最少需要多少步,跳的规则为:可以向四个方向的任意一个方向跳当前格子中的步数,若跳不到右下角输出IMPOSSIBLE。
题解:
BFS搜索,注意判断边界,标记。
代码:
#include <iostream> #include <cstdio> #include <algorithm> #include <stdio.h> #include <cmath> #include <cstring> #include <vector> #include <map> #include <set> #include <bitset> #include <queue> #include <cstdlib> #include <utility> using namespace std; #define is_lower(c) (c>=‘a‘ && c<=‘z‘) #define is_upper(c) (c>=‘A‘ && c<=‘Z‘) #define is_alpha(c) (is_lower(c) || is_upper(c)) #define is_digit(c) (c>=‘0‘ && c<=‘9‘) #define min(a,b) ((a)<(b)?(a):(b)) #define max(a,b) ((a)>(b)?(a):(b)) #define IO ios::sync_with_stdio(0);\ cin.tie(0); cout.tie(0); #define For(i,a,b) for(int i = a; i <= b; i++) typedef long long ll; typedef unsigned long long ull; typedef pair<int,int> pii; typedef pair<int,int > pll; typedef vector<int> vi; const ll inf=0x3f3f3f3f; const double EPS=1e-10; const ll inf_ll=(ll)1e18; const ll maxn=100005LL; const ll mod=1000000007LL; const int N = 500+5; pair <int,int> p; queue <pii> q; int mp[N][N]; int xx[N][N]; bool vis[N][N]; int main() { int m,n; cin >> m >> n; For(i,1,m) For(j,1,n) scanf("%1d",&mp[i][j]); p.first = 1;p.second = 1; q.push(p); vis[1][1] = 1; int sum = 0; while(!q.empty()){ pii x = q.front(); q.pop(); int step = mp[x.first][x.second]; pii x1; if((x.first+step)>=1&&(x.first+step)<=m&&!vis[x.first+step][x.second]){ x1.first = x.first+step,x1.second = x.second; q.push(x1); xx[x1.first][x1.second] = xx[x.first][x.second]+1; vis[x1.first][x1.second] = 1; }//向下 if((x.first-step)>=1&&(x.first-step)<=m&&!vis[x.first-step][x.second]){ x1.first = x.first-step,x1.second = x.second; q.push(x1); xx[x1.first][x1.second] = xx[x.first][x.second]+1; vis[x1.first][x1.second] = 1; }// up if((x.second+step)>=1&&(x.second+step)<=n&&!vis[x.first][x.second+step]){ x1.first = x.first,x1.second = x.second+step; q.push(x1); xx[x1.first][x1.second] = xx[x.first][x.second]+1; vis[x1.first][x1.second] = 1; } if((x.second-step)>=1&&(x.second-step)<=n&&!vis[x.first][x.second-step]){ x1.first = x.first,x1.second = x.second-step; q.push(x1); xx[x1.first][x1.second] = xx[x.first][x.second]+1; vis[x1.first][x1.second] = 1; } if(xx[m][n]!=0) break; } if(xx[m][n]!=0) cout << xx[m][n] <<endl; else cout <<"IMPOSSIBLE" << endl; return 0; }
