目录:
- 什么是因子分析
- 因子分析的作用
- 因子分析模型
- 因子分析的统计特征
- 因子载荷矩阵的估计方法
- 因子旋转
- 为什么要做因子旋转
- 因子旋转方法
- 因子得分
- 因子分析步骤
- 举例
- 因子分析和主成分分析区别
1、什么是因子分析?
因子分析是一种数据简化技术。
- 它通过研究众多变量间的依赖关系,探求观测数据中的基本数据结构,并且用少数几个假象变量(因子)来表示其基本数据结构;
- 这几个假想变量(因子)可以表示原来众多的原始变量的主要信息;
- 原始变量是可观测的显在变量,而假想变量是不可观测的潜在变量,即因子;
即一种用来在众多变量中辨别、分析和归结出变量间的相互关系并用简单的变量(因子)来描述这种关系的数据分析方法
如考察中学生的语文、英语、历史,数学、物理、化学成绩;
- 语文、英语、历史有很强的正相关;
- 数学、物理、化学有很强的正相关;
于是可以提取出两个因子:文科因子和理科因子
2、因子分析的主要作用?
- 寻求基本数据结构
- 数据简化
- 强相关问题会对分析带来困难
- 通过因子分析可以找出少数的几个因子替代原来的变量做回归分析、聚类分析和判别分析
3、因子分析模型

A称为因子载荷矩阵
4、统计特征
因子载荷$a_{ij}$是第i个变量与第j个公共因子的相关系数;
共同度:变量$X_i$的共同度是因子载荷矩阵的第i行的元素的平方和,记为$h_i^2=\sum_{j=1}^{m}a_{ij}^2$;所有的公共因子和特殊因子对变量$X_i$的贡献为1,若$h_i^2$非常接近1,则因子分析的效果好,从原变量空间到公共因子空间的转化性质好;
贡献:因子载荷矩阵中各列元素的平方和$S_j=\sum_{i=1}^p a_{ij}^2$,称为Fj对所有的$X_i$的方差贡献和,衡量Fj的相对重要性;
5、因子载荷矩阵的估计方法
- 主成分分析法
1)得到原始变量的相关系数矩阵;
2)主成分分析,得到特征值和特征向量;
3)确定因子个数(特征根大于1的;碎石原则:特征根从大到小排列,筛掉减小速度变缓的特征根);
4)载荷矩阵等于:特征向量*√(λ_i );
注:主成分分析法忽略了特殊因子。
- 主因子法
- 极大似然法
6、因子旋转(正交变换)

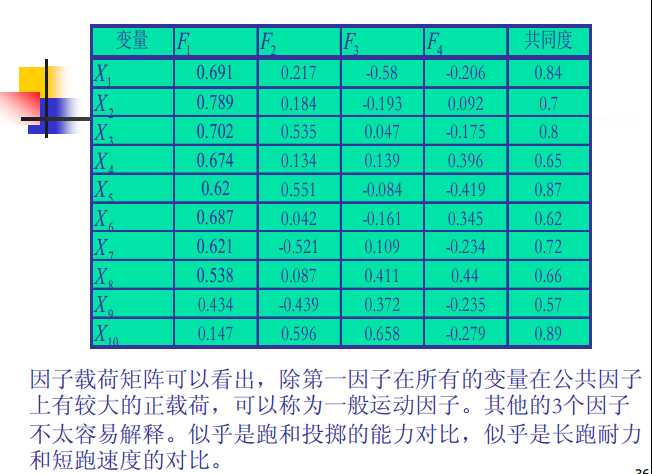
为什么要因子旋转?
- 因子分析的目的不仅仅是要找出公共因子以及对变量进行分组,更重要的是要知道每个公共因子的意义,以便进行进一步的分析。如果每个公共因子的含义不清,则不便于进行实际背景的解释。
- 初始因子的综合性太强,难以找出因子的实际意义。由于因子载荷阵是不唯一的,所以可以对因子载荷阵进行旋转,使因子载荷阵的结构简化,使其每列或行的元素平方值向0和1两极分化。
因子旋转方法
- 方差最大法:使得每个因子上的载荷尽量拉开差距,各自趋向于0,1;
- 四次方最大法:使得每个变量上的载荷尽量拉开差距,各自趋向于0,1;
- 等量最大法:结合上两个方法;
7、因子得分
当我们需要用因子再做分析时,就需要对因子进行测度,给出公共因子的值;
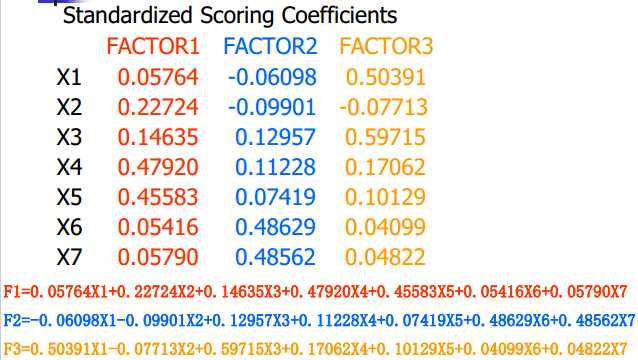
因子得分函数:把因子表示成原变量的线性组合;(得不到精确的值,只能估计)
方法:
- 巴特莱特因子得分(加权最小二乘法)
- 回归方法
8、因子分析步骤
1)选择分析的变量
因子分析的前提条件是观测变量间有较强的相关性,因为如果变量之间没有相关性或者相关性较小的话,他们不会有共享因子;
2)计算所选原始变量的相关系数矩阵
这也是判断所选变量是否有相关关系,如果没有,做因子分析是不恰当的;
3)提取公共因子
需要确定因子求解的方法和因子的数目。跟经验关系很大,一般方差小于1的因子贡献就很弱了,或者累计贡献率可以达到60%;
4)因子旋转
通过坐标变换使得原始变量和尽可能少的因子有密切关系,这样的因子实际意义更易解释;
5)计算因子得分
有了因子得分值,则可以在以后的分析(聚类分析、回归分析)中继续使用因子;
9、举例

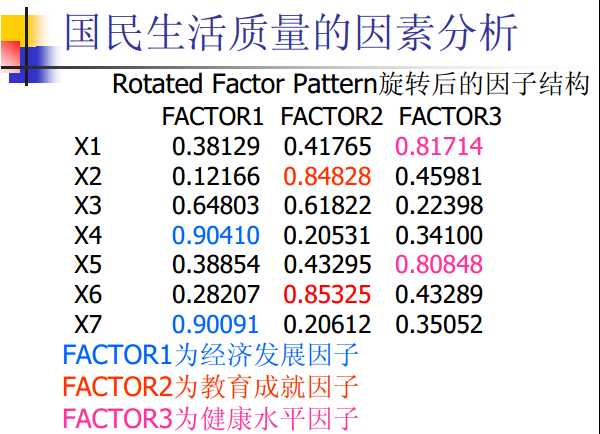
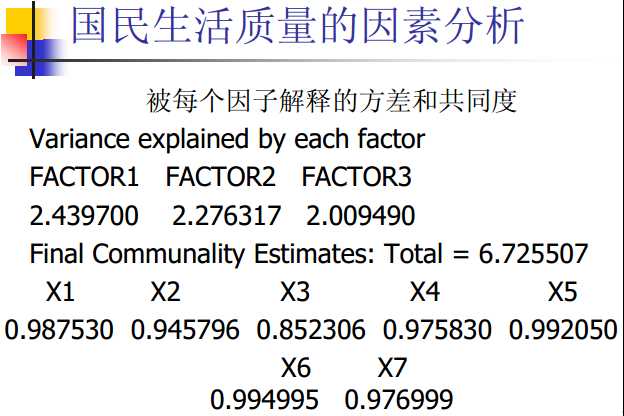
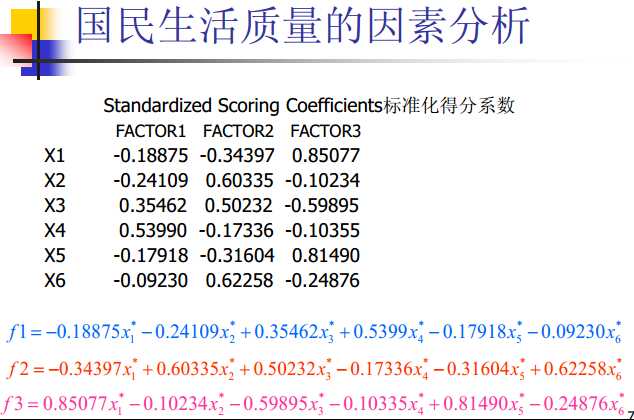
注:
因子分析是十分主观的,得到的因子究竟有什么意义也都是凭借自己的先验知识才可以知道的,所以评价因子分析的质量也很主观了。
10、主成分分析和因子分析的区别
- 主成分分析仅是变量变换,而因子分析需要构造因子模型;
主成分分析是用原始变量的线性组合来表示新的综合变量,即主成分;
而因子分析是用潜在的假想变量和随机影响变量的线性组合来表示原始变量;因子分析除了公共因子外还有特殊因子。
- 由于模型的特点,因子分析还多了”因子旋转“这一步,旋转后的公共因子一般没有主成分那么综合,公共因子往往可以找到实际意义,而主成分一般没有实际意义;
最后:
若数据本身就十分的独立,就很难用少数的变量取表示原始变量,降维可能失败,数据越相关,降维效果越好,可用如下办法进行变量间的相关性检验:
- KMO样本测度:KMO>0.7:适合;KMO<0.5:不适合;
- 巴特莱特球体检验:H0:相关系数矩阵R为单位阵,拒绝H0可作因子分析;
