Description:
Input:
第一行是两个整数N(3 ? N ? 200000)和M,分别表示居住点总数和街道总数。以下M行,每行给出一条街道的信息。第i+1行包含整数Ui、Vi、Ti(1?Ui, Vi ? N,1 ? Ti ? 1000000000),表示街道i连接居住点Ui和Vi,并且经过街道i需花费Ti分钟。街道信息不会重复给出。
Output:
仅包含整数T,即最坏情况下Chris的父母需要花费T分钟才能找到Chris。
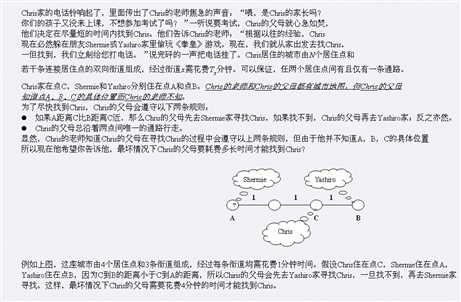
思路:由于规则2,可知题目给出的是一棵树
然后求一根直径,两个家就在直径两端
两端各遍历一发,就可以知道每个点到两端的距离,然后取出每个点到两端的最小距离再加上直径长度即可

#include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; const int N = 1e6 + 10; int head[N], now; struct edges{ int to, next, w; }edge[N<<1]; void add(int u, int v, int w){ edge[++now] = {v, head[u], w}; head[u] = now;} long long n, m, d[N], l, r, f[N]; int bfs(int x){ queue<int> q; memset(d, 0x3f, sizeof(d)); q.push(x); d[x] = 0; while(!q.empty()){ int x = q.front(); q.pop(); for(int i = head[x]; i; i = edge[i].next){ int v = edge[i].to; if(d[v] > d[x] + edge[i].w){ d[v] = d[x] + edge[i].w; q.push(v); } } } for(int i = 1; i <= n; i++) if(d[i] > d[x]) x = i; return x; } int main(){ scanf("%lld%lld",&n, &m); int x, y, z; for(int i = 1; i <= m; i++){ scanf("%d%d%d",&x, &y, &z); add(x, y, z); add(y, x, z); } l = bfs(1); r = bfs(l); memcpy(f, d, sizeof(d)); bfs(r); long long mx = 0; for(int i = 1; i <= n; i++) mx = max(mx, min(d[i], f[i])+ f[r]); printf("%lld\n", mx); return 0; }

