传送门
题目描述
司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
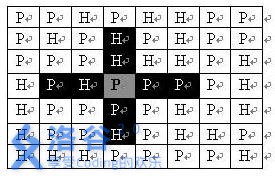
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
思路
首先可以看出这是一道状压dp,然后具体思考如何进行状压,首先可以想到用四进制表示离中心的位置,然后每一行向下扫,向下扫的时候利用四进制数进行状态转移,如11表示离中心距离为3,是可以放的,10表示2,10表示1,00表示中心,但是仔细想想会发现这种做法无论在时间,空间,还是代码实现难度上都是难以实现的,所以就要换一种思路考虑。
多谢瑞屎爷的帮助,才过了这道题2333333
其实这道题用二进制就可以了,用1表示这个位置上放了炮兵。我们可以观察到,每个炮兵的影响位置有两个,所以我们要枚举前两行的状态,我们一横行一横行向下扫,用1表示这个这个位置放了炮兵。
dp[i][j][k]表示当前选到了第i行,当前的状态为j时,前一行的的状态为k时的最大数量,所以有4重循环,由上一行枚举到这一行。
注意
这道题如果直接写状压的的话,状态会非常多,数组会炸,空间也会炸O(∩_∩)O。我们发现,同一行至少间隔两个格子才能放一个炮兵,所以允许的状态要比原有的少很多,我们首先预处理出所有的状态,发现只有不到100种,好像是88种╮(╯▽╰)╭
所以时间上不会爆炸233333
用vector数组记录一下所有的情况。
在枚举的时候,还要注意到以下几点:
1.要判断每个状态能否放置在地图上
2.要判断每个状态的炮兵能否互相打到
3.用来转移的前一种状态是否存在
代码
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<vector> 6 using namespace std; 7 vector<int>v; 8 int N,M; 9 bool map[200][200]; 10 int check[300]; 11 int dp[200][200][200]; 12 int val[300]; 13 inline bool judge (int a){ //判断这种状态自己行内的炮兵能否互相打到 14 if((a&(a<<1)))return false; 15 if((a&(a<<2)))return false; 16 else return true; 17 } 18 inline int calc(int x){ //计算每种情况的炮兵个数 19 int ans=0; 20 while(x){ 21 if(x&1)ans++; 22 x=x>>1; 23 } 24 return ans; 25 } 26 int main(){ 27 memset(dp,-1,sizeof(dp)); 28 cin>>N>>M; 29 int tot=(1<<M)-1; 30 int shu=0; 31 for(register int i=0;i<=tot;i++){ //预处理出所有可能的状态并用vector数组记录 32 if(judge(i)){ 33 v.push_back(i); //用vector数组记录情况 34 val[shu]=calc(i); //用val数组记录当前情况有多少个炮兵 35 shu++; 36 } 37 } 38 char temp; 39 for(register int i=1;i<=N;i++){ 40 for(register int j=1;j<=M;j++){ 41 cin>>temp; 42 if(temp==‘P‘)map[i][j]=1; 43 else map[i][j]=0; 44 check[i-1]+=(map[i][j]<<(j-1)); //生成地图的二进制形式,如果为1,则可以放炮兵 45 } 46 } 47 int cnt=v.size()-1; 48 for(register int i=0;i<=cnt;i++){ 49 if((v[i]|check[0])==check[0]){ 50 dp[0][i][0]=val[i]; //初始化dp数组,第0列不受前面列的影响,因此每种状态的初始值就是这种状态的炮兵数量 51 } 52 } 53 for(register int i=1;i<N;i++){ //枚举行 54 for(register int j=0;j<=cnt;j++){ // 枚举当前状态 55 if((v[j]|check[i])!=check[i])continue; //判断当前的状态能否在地图上放置 56 for(register int l=0;l<=cnt;l++){ //枚举上一行的状态 57 if(v[l]&v[j])continue; //判断前一行的炮兵能否打到当前行的炮兵 58 if((v[l]|check[i-1])!=check[i-1])continue; //判断前一行的炮兵能否放在地图上 59 for(register int ll=0;ll<=cnt;ll++){ // 枚举上一行的上一行的状态 60 if(dp[i-1][l][ll]==-1)continue; //判断上一种情况是否存在 61 if(v[ll]&v[j])continue; //判断两行前的炮兵会不会达到当前行的炮兵 62 if(v[ll]&v[l])continue; //判断两行前的炮兵会不会达到上一行的炮兵 63 if((v[ll]|check[i-2])!=check[i-2])continue; //判断两行前的炮兵能否放置在地图上 64 dp[i][j][l]=max(dp[i-1][l][ll]+val[j],dp[i][j][l]); //状态转移 65 } 66 } 67 } 68 } 69 int ans=0; 70 for(register int i=0;i<=cnt;i++){ 71 for(register int j=0;j<=cnt;j++){ 72 ans=max(dp[N-1][i][j],ans); //因为要求最大值,所以枚举最后一行的所有状态的人数,取最大值 73 } 74 } 75 cout<<ans<<endl; 76 }
