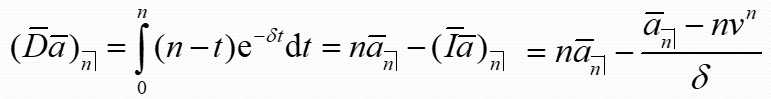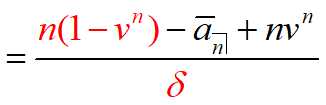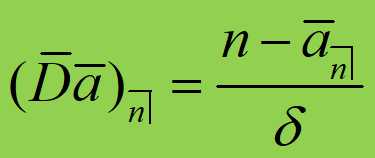一、
现值:付款从时刻 a 到时刻 b,在时刻 t 的付款率为ρt,利息力为 δ。
时刻 t支付的1在时刻0的现值为:
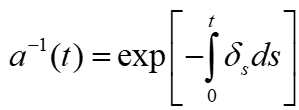
在时刻 t 的付款率为ρt,所有付款在时刻0的现值是将所有付款的现值加总:
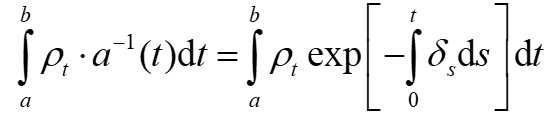
二、
终值:在时刻 t 的1元,累积到时刻 T 的终值为
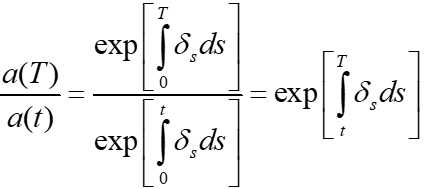
从时刻a到时刻b内所有付款到时刻 T 的终值,就是将该期间内所有付款的终值加总:
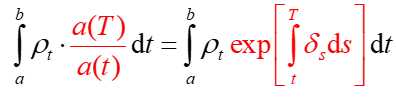
三、连续递增年金(continuously increasing annuity)
假设在时刻t的付款率(payment rate)为 t,常数利息力为δ,则连续递增年金的现值为:
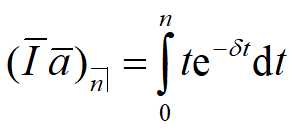
例:
一项10年期的年金,在时刻 t 的付款率为9t+6,利息力为9%,请计算此项年金在时刻零的现值。
解:
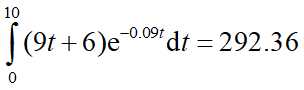
连续递增的永续年金:
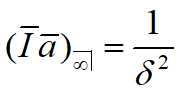
四、连续递减年金 (continuously decreasing annuity)
含义:支付期为 n 年,在时刻 t 的付款率为 n- t,固定利息力为d。现值为: