算法
正向最大匹配法;
基于最大概率分词方法
数据结构
在本次实验中最重要的事情就是建立合理的字典的索引结构,使得查询的速度、存储的空间需求达到较好的性能。
通过观察字典内容可知,存在多个词语有相同前缀的情况,而且数目是比较多的。如果按照直观的思想,直接将所有的词语保存在一个数据组中以供检索时候使用,势必造成
巨大的内存资源浪费,其二还会降低检索的效率。
对于词典中的数据采用词典树来保存时比较好的数据结构,它比较好的解决了公共前缀的困扰。但是存在一个问题,即从根到所有终止节点所代表的词语不一定是词典中的数
据。这里我们通过在节点中增添一个flag标志位来解决这个问题。
词典树结构定义如下:
private String str;// 保存词的内容 private int frequency = -1;//频率 private double probability=-1;//出现的概率 private int flag;//标记从跟到此节点的字符串是否是字典词 private Map<String, Tree> children;//孩子序列
注意:这里的private int frequency = -1;//频率 private double probability=-1;//出现的概率 private int flag;//标记从跟到此节点的字符串是否是字典词 三个属性在正向最大匹配时没有用到,这是在基于最概率大方法中所需要的。
算法实现
正向最大匹配算法:
正向最大匹配算法的要求:应该尽可能的将词语划分最大的长度。即应该按照字典中的顺序应该从最大长度的词语开始查起,匹配则划分,不匹配则长度减一,继续查找,直
到匹配长度为1(存在则为字典单字,不存在为非字典字)或者找到匹配为止(长度大于1的词典词)。
在词典树的数据结构中,不需要从最长的词语开始查找。因为字典中所有的词都是从树的根节点开始的,到树中的某一个节点停止。我们要做就是尽可能的向下遍历节点,当
到达叶节点或者找不到对应的节点时,应该回溯查找已经存在的最长词的划分。(详见代码),然后进行从头的再次开始查找。
基于最大概率的中文分词:
基本思想:
最大概率分词就是要求得 Max(P(w1|s),P(w2|s)) 。根据贝叶斯公式:P(w|s)=P(s|w)P(w)/P(s)(公式1)。在公式1中,因为P(s)和P(w|s)都基本一样,因此,就求最大的P(w)即可。根据一元语法,词之间出现的概率互相独立,因此有下面的公式成立: P(w)=P(w1,w2,…,w3)=P(w1)P(w2)…P(w3)即字符串出现的概率就是构成字符串的各个词的概率之积。
而一个词的概率可以按照其出现的次数除以语料中总的词数得到。在实际操作中可以发现P(w)与log(p(w))具有相同的性质(增大而增大)。我们可以将判断的依据改为使得log(w)=log(p(w1))+……+log(p(wn))的最大值,这样我们就将所求的问题转化为和最大的问题。
如果我们将p(w)定义为p(w)=总频数/频数。这样我们判断的依据就是使得:log(w)=log(p(w1))+……+log(p(wn))最小的组合。
至此,我们已经将问题转化为在图结构中的最短路径问题。图的顶点是句子中出现的词典词语,权值是相对的log(p(w))。
算法步骤:
1:构造字典树;
2:构造图结构;
3:寻找最短路径;
4:输出结果
算法存在的问题:
1:构成句子的所有字都必须出现在词典词典中,否则算法出错。
2:由于在求最短路径时,需要分配NN的数组,所有对于大规模的文本可能出现内存不足的错误情况。
实验结果:
正向最大匹配:
输入:
str="一下子一九七二年"
输出:
str="一下子/一九七二年"
最大概率分析的结果:
使用的字典实例:
20 //词频的总数 今 1 //词的频率 天 1 雨 1 今天 12 下雨 3 天下 2
测试句子:
str="今天下雨"
字母相对应的频数(代替log(p(w))):
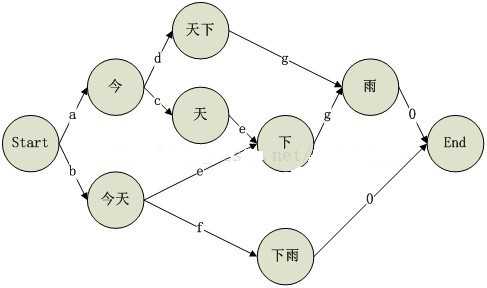
输出结果:
今天/下雨
代码:
完整代码详见:
https://github.com/BFH1122/Chinese_Seg
正向最大匹配法
构造字典树:
package com; import java.util.HashMap; import java.util.Map; public class Tree { private String str;// private int frequency = -1;//频率 private double probability=-1;//出现的概率 private int flag;//标记从跟到此节点的字符串是否是字典词 private Map<String, Tree> children;//孩子序列 public int getFlag() { return flag; } public void setFlag(int flag) { this.flag = flag; } public String getStr() { return str; } public void setStr(String str) { this.str = str; } public int getFrequency() { return frequency; } public void setFrequency(int frequency) { this.frequency = frequency; } public double getProbability() { return probability; } public void setProbability(double probability) { this.probability = probability; } public void addChild(Tree node) { if (children == null) { children = new HashMap<String, Tree>(); } if (!children.containsKey(node.getStr())) { children.put(node.getStr(), node); } } public Tree getChild(String ch) { if (children == null || !children.containsKey(ch)) { return null; } return children.get(ch); } public Map<String,Tree> getAllChilden() { return this.children; } public void removeChild(String ch) { if (children == null || !children.containsKey(ch)) { return; } children.remove(ch); } }
分析算法:
package com; import java.io.BufferedReader; import java.io.File; import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.IOException; import java.io.InputStreamReader; import java.io.UnsupportedEncodingException; import java.util.ArrayList; import java.util.List; import java.util.Map; public class Latex { public int Max=999999; private Tree root=null; public Latex(String file) throws IOException { BuildTree(file); } public void Print() { } //图的节点的属性 public class Node{ public int id; public String str;//保r存节点上的字符 public double cost; public String pro_str; public String next_str; } public Tree getNodeByWord(String word) { if (root == null) { System.out.println("发生错误!"); return null; } Tree node = root; for (int i = 0; i < word.length(); i++) { String ch = word.charAt(i) + ""; if (node == null) { break; } else { node = node.getChild(ch); } } return node; } public List<Node> BuildTu(String sentence) { List<Node> Segs = new ArrayList<Node>(); Node start_node=new Node(); start_node.pro_str="-1"; start_node.next_str="-1"; start_node.id=0; start_node.str="start"; Segs.add(start_node); int tmp_id=0; for (int i = 0; i < sentence.length(); i++) { for (int j = i + 1; j <= sentence.length(); j++) { String word = sentence.substring(i, j); Tree tmp_node = this.getNodeByWord(word); if (tmp_node == null) { break; } if (tmp_node.getFrequency() <= 0) { continue; } Node seg = new Node(); seg.str = word; seg.id=tmp_id++; seg.next_str = word.substring(word.length() - 1, word.length()); if (i == 0) { seg.pro_str="-1"; } else { seg.pro_str = sentence.substring(i - 1, i); } seg.cost = tmp_node.getProbability(); Segs.add(seg); } } Node end_node=new Node(); end_node.id=tmp_id++; end_node.cost=1; end_node.pro_str=sentence.substring(sentence.length()-1,sentence.length()); end_node.next_str="-1"; end_node.str="end"; Segs.add(end_node); return Segs; } // public void search_path(List<Node> Segs) { if(Segs.size()==0) return; int N=Segs.size(); double COST[][]=new double[N][N]; for(int i=0;i<N;i++) { for(int j=0;j<N;j++) COST[i][j]=Max;//初始化为最大值 } for(int i=0;i<N;i++) { Node tmp_node=Segs.get(i); for(int j=0;j<N;j++) { Node ttmp=Segs.get(j); if(tmp_node.next_str.equals(ttmp.pro_str)) { COST[i][j]=ttmp.cost; // System.out.println(tmp_node.str+" "+i+"->"+j+" "+ttmp.str); } } } int dex_path[]=new int[N]; dex_path[0]=-1; String path[]=new String[N]; for(int i=1;i<N;i++) { dex_path[i]=0; } List<Integer> S = new ArrayList<Integer>(); S.add(0); List<Integer> T=new ArrayList<Integer>(); double distance[]=new double[N]; for(int i=1;i<N;i++) { T.add(i); if(COST[0][i]<Max) distance[i]=COST[0][i]; else distance[i]=Max; } while(!T.isEmpty()) { double min=distance[T.get(0)]; int k=T.get(0); int kk=0; for(int i=0;i<T.size();i++) { if(distance[T.get(i)]<min) { min=distance[T.get(i)]; k=T.get(i); kk=i; } } T.remove(kk); //更改权值 for(int i=0;i<N;i++) { if(distance[i]>distance[k]+COST[k][i]) { distance[i]=distance[k]+COST[k][i]; dex_path[i]=k; } } } String path_str=""; int x=dex_path[N-1]; while(x!=-1) { path_str=Segs.get(x).str+"/"+path_str; x=dex_path[x]; } System.out.println(path_str.substring(6,path_str.length())); } //依概率的方式进行分析 public String Latex_str(String str) { String result=""; search_path(BuildTu(str)); return result; } //建立字典树 public void BuildTree(String file_name) throws IOException { root=new Tree(); File file = new File(file_name); BufferedReader in = new BufferedReader( new InputStreamReader(new FileInputStream(file), "utf-8"));//??????? String line = in.readLine();//读入第一行,是词典词的总频数 int totalFreq = Integer.parseInt(line); while((line=in.readLine())!=null) { Tree node=root; String[] segs = line.split("\t"); String word = segs[0]; int freq=-1; freq = Integer.parseInt(segs[1]);//读取词频 for(int i=0;i<word.length();i++) { char ch=word.charAt(i); Tree tmp_node=node.getChild(""+ch); if(tmp_node==null) { tmp_node=new Tree(); tmp_node.setStr(ch+""); node.addChild(tmp_node); } node=tmp_node; } node.setFlag(1); node.setFrequency(freq); node.setProbability(Math.log((double)totalFreq / freq)); } in.close(); } }
