GloVe损失函数的理解

时间：2018-04-07 13:55:56 阅读：734 评论：0 收藏：0 [点我收藏+]

简介

GloVe是一种非常简单快速的训练词向量的算法。与复杂的word2vec相比，其是一个log双线性模型，仅通过一个简单的损失函数就能够得到很好的结果。

\begin{matrix} (1) & J = \sum_{i, j}^{N} f (X_{i, j}) (v_{i}^{T} v_{j} + b_{i} + b_{j} - l o g (X_{i, j}))^{2} \end{matrix}

其中， $v_{i}$ 和 $v_{j}$ 是i和j的词向量， $b_{i}$ 和 $b_{j}$ 是两个偏差项， $f$ 是一个权重函数，N为词汇表大小
但是这个损失函数的意义却不是很直观，这里参照一篇博客写了一下对于这个损失函数的分析

思路

Glove首先会通过设置定义的窗口大小，进行统计得到词的共现矩阵。如 $X_{i, j}$ 表示词 $i$ 和 $j$ 同时出现的次数。共现矩阵是一个 $N \times N$ 的矩阵

然后我们需要计算一些条件概率
定义

X_{i} = \sum_{j = 1}^{N} X_{i, j}

P_{i, k} = \frac{X_{i, k}}{X_{i}}

r a t i o_{i, j, k} = \frac{P_{i, k}}{P_{j, k}}

然后我们分析这里的ratio会发现一些规律

技术分享图片
所以我们想到，如果能够通过词向量 $v_{i}$ , $v_{j}$ 和 $v_{k}$ 得到相似的规律的，那么说明我们的词向量是很不错的。即我们想做的是得到函数 $g ()$ ，使之满足

r a t i o_{i, j, k} = \frac{P_{i, k}}{P_{j, k}} = g (v_{i}, v_{j}, v_{k})

那么为了使二者尽量想近，对于损失函数，一个直观的想法就是MSE，即

\begin{matrix} (2) & J = \sum_{i, j, k}^{N} (\frac{P_{i, k}}{P_{j, k}} - g (v_{i}, v_{j}, v_{k}))^{2} \end{matrix}

不过这里的计算复杂度是 $N^{3}$ ，过于复杂，我们需要进一步分析。我们可以开始猜想一下 $g (v_{i}, v_{j}, v_{k})$ 是一个什么样的形式，因为其衡量了单词i，j之间的关系，那么我们可以猜想其中含有 $v_{i} - v_{j}$ ，又因为其中还有对k的关系且最终是一个标量，那么我们假设其存在一个内积，即 $(v_{i} - v_{j})^{T} v_{k}$
那么现在我们有

\frac{P_{i, k}}{P_{j, k}} = g (v_{i}, v_{j}, v_{k}) = (v_{i} - v_{j})^{T} v_{k} = v_{i}^{T} v_{k} - v_{j}^{T} v_{k}

可以看到这里我们和上面的损失函数有点类似了，但是还是缺少一个 $\exp$ ，我们可以加上它看看，即

\frac{P_{i, k}}{P_{j, k}} = \exp (v_{i}^{T} v_{k} - v_{j}^{T} v_{k}) = \frac{\exp (v_{i}^{T} v_{k})}{\exp (v_{j}^{T} v_{k})}

可以看到，加上 $\exp$ 之后分子分母的形式就完全一样了，我们可以将其一起考虑，即现在只需要满足

P_{i, j} = e x p (v_{i}^{T} v_{j})

两边取对数，我们的损失函数就能够转化为

\begin{matrix} (3) & J = \sum_{i, j}^{N} (l o g (P_{i, j}) - v_{i}^{T} v_{j})^{2} \end{matrix}

这个损失函数已经更像一些了，但是还是不太一样。这是因为我们前面是存在一点问题的。根据前面我们有

l o g (P_{i, j}) = v_{i}^{T} v_{j} 和 l o g (P_{j, i}) = v_{j}^{T} v_{i}

但是实际上，上面的式子右边是相等的，但左边并不相等（并且对于这个问题来说，我们可以想到target和context其实是可以互换的，所以存在对称），即原有的对称性不满足了。我们需要进一步处理一下。我们将上面(3)的中的条件概率 $l o g (P_{i, j})$ 展开，得到

l o g (P_{i, j}) = l o g (X_{i, j}) - l o g (X_{i}) = v_{i}^{T} v_{j}

这里的 $l o g (X_{i})$ 是独立于j的，所以可以被吸收进 $b_{i}$ 变为

l o g (X_{i, j}) = v_{i}^{T} v_{j} + b_{i} + b_{j}

这样代价函数就变成了

J = \sum_{i, j}^{N} (v_{i}^{T} v_{j} + b_{i} + b_{j} - l o g (X_{i, j}))^{2}

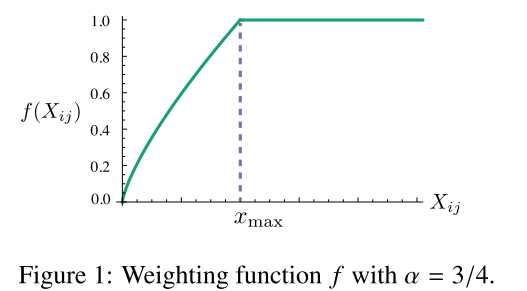
然后加上词频越高权重越大（共现次数很少的实际上很可能是异常值，并且共现次数少的一般来说含的信息也少）

\begin{matrix} (4) & J = \sum_{i, j}^{N} f (X_{i, j}) (v_{i}^{T} v_{j} + b_{i} + b_{j} - l o g (X_{i, j}))^{2} \end{matrix}

权重函数

f (x) = {\begin{cases} (x / x m a x)^{0.75}, & if x < x m a x \\ 1, & if x >= x m a x \end{cases}

技术分享图片

引用

Pennington J, Socher R, Manning C. Glove: Global vectors for word representation[C]//Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP). 2014: 1532-1543.
https://blog.csdn.net/codertc/article/details/73864097

<wiz_tmp_tag id="wiz-table-range-border" contenteditable="false" style="display: none;">

来自为知笔记(Wiz)

GloVe损失函数的理解

标签：ioi 词向量 pac enc min nali 技术分享 ima 出现

原文地址：https://www.cnblogs.com/MrLJC/p/8732985.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行