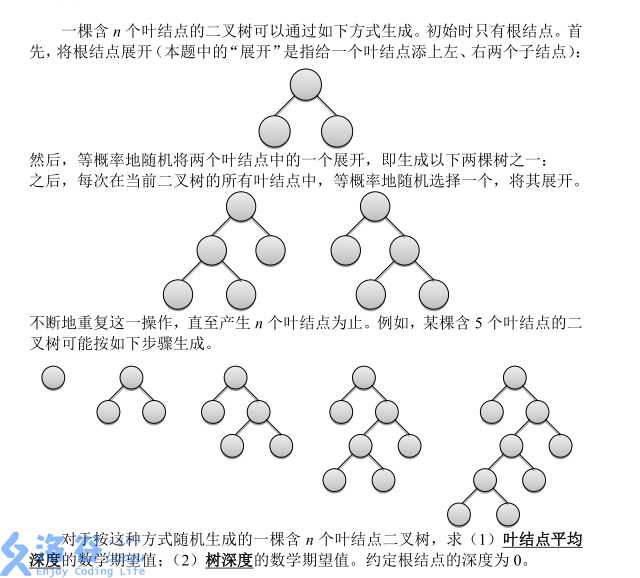
题目
输入格式
输入仅有一行,包含两个正整数 q, n,分别表示问题编号以及叶结点的个数。
输出格式
输出仅有一行,包含一个实数 d,四舍五入精确到小数点后 6 位。如果 q = 1,则 d 表示叶结点平均深度的数学期望值;如果 q = 2,则 d 表示树深度的数学期望值。
输入样例
1 4
输出样例
2.166667
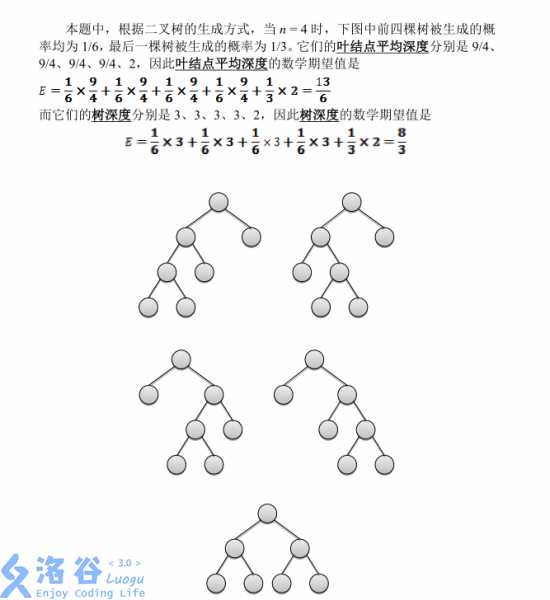
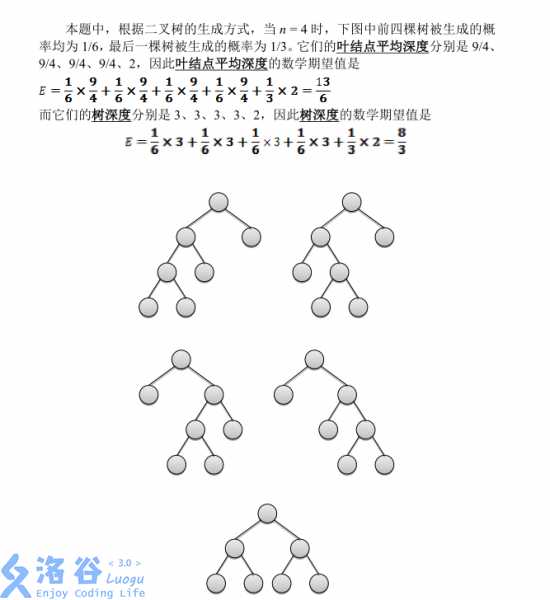
提示

题解
第一问比较简单,我们设\(f[i]\)表示第\(i\)次扩展的期望深度
那么\(f[i] = \frac{f[i - 1] * (i - 2) + (f[i - 1] + 1) * 2}{i}\)
化简得\(f[i] = f[i - 1] + \frac{2}{i}\)
第二问
首先我们有这样一个整数概率公式:\(E(x) = \sum_{i = 1}^{+\infty} P(x >= i)\)
含义为:随机变量\(x\)的期望为所有\(x>=i\)的概率之和
那我们设\(f[i][d]\)表示有\(i\)个叶子,深度\(>=d\)的概率,
那么\(ans = \sum_{i = 1}^{n - 1} f[n][i]\)
考虑转移,我们枚举左右子树分到多少叶子
\(f[i][d] = \sum_{j = 1}^{i - 1} \frac{f[j][d - 1] + f[i - j][d - 1] - f[j][d - 1]*f[i - j][d - 1]}{i - 1}\)
其实就是一个容斥,两边都大于\(d - 1\)的部分会被算两次,减去一次即可
这样我们就做完了
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<‘ ‘; puts("");
using namespace std;
const int maxn = 205,maxm = 100005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == ‘-‘) flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
double f[maxn][maxn];
int n,t,m;
void solve1(){
double ans = 0;
for (int i = 2; i <= n; i++){
ans += 2.0 / i;
}
printf("%.6lf\n",ans);
}
void solve2(){
for (int i = 1; i <= n; i++) f[i][0] = 1;
for (int i = 2; i <= n; i++){
for (int d = 1; d < i; d++){
for (int j = 1; j < i; j++)
f[i][d] += (f[j][d - 1] + f[i - j][d - 1] - f[j][d - 1] * f[i - j][d - 1]) / (i - 1);
}
}
double ans = 0;
for (int i = 1; i < n; i++) ans += f[n][i];
printf("%.6lf\n",ans);
}
int main(){
t = read(); n = read();
if (t & 1) solve1();
else solve2();
return 0;
}