参考:
L1 Norm Regularization and Sparsity Explained for Dummies 专为小白解释的文章,文笔十分之幽默
- why does a small L1 norm give a sparse solution?
- why does a sparse solution avoid over-fitting?
- what does regularization do really?
减少feature的数量可以防止over fitting,尤其是在特征比样本数多得多的情况下。
L1就二维而言是一个四边形(L1 norm is |x| + |y|),它是只有形状没有大小的,所以可以不断伸缩。我们得到的参数是一个直线(两个参数时),也就是我们有无数种取参数的方法,但是我们想满足L1的约束条件,所以 要选择相交点的参数组。
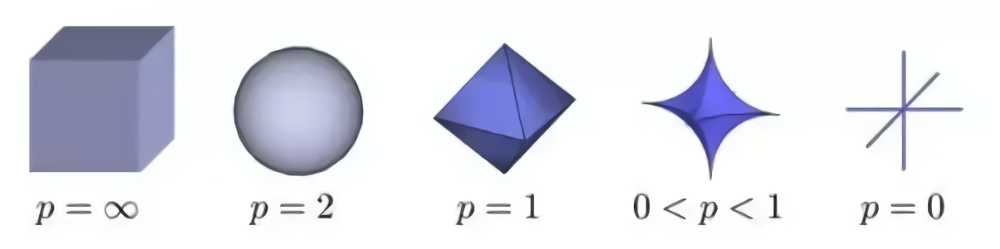
Then why not letting p < 1? That’s because when p < 1, there are calculation difficulties. 所以我们通常只在L1和L2之间选,这是因为计算问题,并不是不能。
l0-Norm, l1-Norm, l2-Norm, … , l-infinity Norm
where
就是一个简单的公式而已,所有的范数瞬间都可以理解了。(注意范数的写法,写在下面,带双竖杠)
Before answering your question I need to edit that Manhattan norm is actually L1 norm and Euclidean norm is L2.
As for real-life meaning, Euclidean norm measures the beeline/bird-line distance, i.e. just the length of the line segment connecting two points. However, when we move around, especially in a crowded city area like Manhattan, we obviously cannot follow a straight line (unless you can fly like a bird). Instead, we need to follow a grid-like route, e.g. 3 blocks to teh west, then 4 blocks to the south. The length of this grid route is the Manhattan norm.
之前的印象是L1就是Lasso,是一个四边形,相当于绝对值。
L2就是Ridge,相当于是一个圆。
