6.凑算式

声明

可能本文章会有错误，希望各位读者看到后，记得回复留言，提醒我，以免误人子弟。本人菜鸡，还望各位大佬手下留情。

题目：

凑算式

 B      DEF

A + --- + ------- = 10
C GHI

（如果显示有问题，可以参见【图1.jpg】）

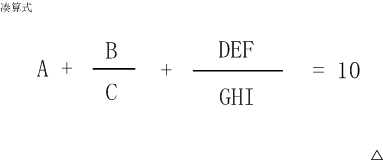
这个算式中A~I代表1~9的数字，不同的字母代表不同的数字。

比如：
6+8/3+952/714 就是一种解法，
5+3/1+972/486 是另一种解法。

这个算式一共有多少种解法？

注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。

分析：

这道题需要用到全排列，如果不太会的还是要去看下全排列。
将ABCDEFGHI全排列组合一边，然后选出满足条件的。
需要注意的是比较的位置，如果是int型，结果会自动取整

代码

public class f {
    //总共解法次数
    static int count = 0;
    public static void cou(int[] list) {
        //将结果比较，这里需要注意将后面的数转为double型，与double型的10.0比较
        double result = list[0] + 1.0*list[1]/list[2] + 1.0*(list[3]*100+list[4]*10+list[5])/(list[6]*100+list[7]*10+list[8]);
        if(result == 10.0)
            count++;
    }
    
    
    //这里全排列运用的递归
    //list:数组,begin:开始的位置，length:长度
    public static void fun(int[] list,int begin,int length) {
        //如果开始的位置等于数组长度，那么
        if(begin==length) {
            cou(list);
        }else {
            for(int i=begin;i<=length;i++) {
                //交换两个数
                swap(list,begin,i);
                //递归
                fun(list,begin+1,length);
                //再将两个数交换回来
                swap(list,begin,i);
            }
        }
    }
    
    //交换两个数函数
    public static void swap(int[] list,int a,int b) {
        int temp = list[a];
        list[a] = list[b];
        list[b] = temp;
    }
    
    
    
    public static void main(String[] args) {
        int[] list = {1,2,3,4,5,6,7,8,9};
        fun(list,0,list.length-1);
        System.out.println(count + "次");
    }
}