题目链接:
https://vjudge.net/problem/POJ-1556
题目大意:
给一个10*10的正方形房间中间用墙隔开每个墙上有两个门,给出门的两个端点坐标求从左边中点走到右边中点所需要的最短路程。
思路:
每扇门4个点,只要求出每两点之间的距离就可以建图求最短路径了,但是关键在于如何判断两点之间有没有直接路径,即两点之间呢能否直接连接,这就需要判断线段之间的相交问题,每堵墙有两个门,这堵墙被分成三部分,再判断两点之间有没有直接的路的时候,需要判断两点之间有没有和墙壁相交
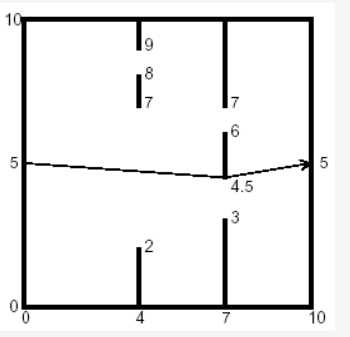
比如上面的例子,第一堵墙分成了三部分,分别是:
(4,0)-(4,2)
(4,7)-(4,8)
(4,9)-(4,10)
判断两个点和墙的每一部分的是否相交时候,需要判断墙的两个端点是否在判断的那两个点的线段的同一侧。具体实现看代码,以后整理出计算几何入门必备模板。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<queue> 7 #include<stack> 8 #include<map> 9 #include<set> 10 #include<sstream> 11 using namespace std; 12 typedef long long ll; 13 const int maxn = 1e2 + 10; 14 const int INF = 1e9 + 7; 15 int T, n, m, cases; 16 struct Point 17 { 18 double x, y; 19 Point(double x, double y):x(x), y(y){} 20 Point(){} 21 }; 22 struct Wall 23 { 24 double x, y[4]; 25 }; 26 Point p[maxn];//存储每个点 27 Wall w[20];//存储每堵墙,墙的x升序,y升序 28 double Map[maxn][maxn];//邻接矩阵 29 double Dis(Point a, Point b)//求两点之间的距离 30 { 31 return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 32 } 33 //判断点c位于直线ab上方还是下方 34 //矢量AB叉乘AC,大于0说明C在AB上方,小于0C在AB下方 35 //(b.x-a.x, b.y-a.y)叉乘(c.x-a.x, c.y-a.y) 36 double Judge_Cross(Point a, Point b, Point c) 37 { 38 return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y); 39 } 40 bool Isok(Point a, Point b)//判断点a, b是否有直接的路 41 { 42 if(a.x >= b.x)return false; 43 int i = 0, flag = true; 44 while(w[i].x <= a.x && i < n)i++;//排除x坐标比a小的墙 45 while(w[i].x < b.x && i < n) 46 { 47 if(Judge_Cross(a, b, Point(w[i].x, 0)) * Judge_Cross(a, b, Point(w[i].x, w[i].y[0])) < 0)//点a,b被第一段阻挡 48 { 49 flag = false; 50 break; 51 } 52 if(Judge_Cross(a, b, Point(w[i].x, w[i].y[1])) * Judge_Cross(a, b, Point(w[i].x, w[i].y[2])) < 0) 53 { 54 flag = false; 55 break; 56 } 57 if(Judge_Cross(a, b, Point(w[i].x, w[i].y[3])) * Judge_Cross(a, b, Point(w[i].x, 10)) < 0) 58 { 59 flag = false; 60 break; 61 } 62 i++; 63 } 64 return flag; 65 } 66 int tot; 67 double dijkstra(int u, int v) 68 { 69 int vis[maxn]; 70 double d[maxn]; 71 memset(vis, 0, sizeof(vis)); 72 for(int i = 0; i < tot; i++)d[i] = INF * 1.0; 73 d[u] = 0; 74 for(int i = 0; i < tot; i++) 75 { 76 int x; 77 double m = 1.0 * INF; 78 for(int i = 0; i < tot; i++)if(!vis[i] && m > d[i])m = d[x = i]; 79 vis[x] = 1; 80 for(int i = 0; i < tot; i++)d[i] = min(d[i], d[x] + Map[x][i]); 81 } 82 return d[v]; 83 } 84 85 int main() 86 { 87 while(cin >> n && (n != -1)) 88 { 89 p[0] = Point(0, 5); 90 tot = 1; 91 for(int i = 0; i < n; i++) 92 { 93 cin >> w[i].x; 94 for(int j = 0; j < 4; j++) 95 { 96 cin >> w[i].y[j]; 97 p[tot++] = Point(w[i].x, w[i].y[j]); 98 } 99 } 100 p[tot++] = Point(10, 5); 101 for(int i = 0; i < tot; i++)//初始化邻接矩阵 102 { 103 for(int j = 0; j < tot; j++) 104 Map[i][j] = 1.0 * INF; 105 } 106 //for(int i = 0; i < tot; i++)cout<<p[i].x<<" "<<p[i].y<<endl; 107 108 for(int i = 0; i < tot; i++)//建图 109 { 110 for(int j = i + 1; j < tot; j++) 111 { 112 if(Isok(p[i], p[j]))//点i和点j有直接的路就建图 113 { 114 Map[i][j] = Dis(p[i], p[j]); 115 //cout<<i<<" "<<j<<" "<<Map[i][j]<<endl; 116 } 117 } 118 } 119 printf("%.2f\n", dijkstra(0, tot - 1)); 120 } 121 return 0; 122 }
