标签:bic 部分 失败 路径 image 贝叶斯定理 准确率 img 导数
一、贝叶斯定理
机器学习所要实现的均是通过有限的训练样本尽可能的准确估计出后验概率,也就是所说的结果情况。大题分为判别式模型和生成式模型。
1. 判别式模型:直接通过建模P(结果|特征)的方式来预测结果,典型代表如决策树,BP神经网络、支持向量机等。
2. 生成式模型:先对联合概率分布P(特征,结果)进行建模,然后通过下面的公式得到P(结果|特征),贝叶斯就是通过这种方法来解决问题。
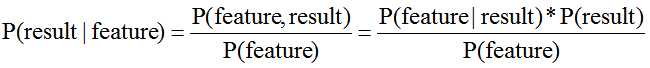
当然贝叶斯的本质公式并不是这个,为了机器学习理解方便,所以就这么拼写,一目了然。
其中P(result)作为类先验概率,P(feature|result)是特征对于结果的类条件概率(似然),所以对于根据特征求结果的学习,就转变成了利用训练数据估计--先验P(resuult)--P(feature|result)的过程。
P(result)表示结果在训练样本中所占的比例,通过统计各类样本出现的频率即可很好的带入计算。
P(feature|result)可就不太一样了,我们往往可能有很多个特征值,这样就会导致,产生这一系列特征值的样本几乎没有,换句话讲:特征值的排列组合往往远远大于训练样本数目,所以单单通过统计是绝对不行的。同样P(feature)也因为相同原因而无法计算。
二、类条件概率的变形(朴素贝叶斯)
朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。简单来说,就是将类条件概率进行拆分,这里采用拆分成连乘的形式:
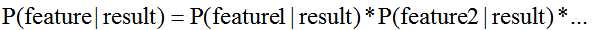
同样P(feature)因为是定值所以并不做考虑的范围内。实际上,预测结果的判断就是比较P(result)*P(feature|result)的大小。
但是当某个概率会特别小的时候,计算机无法判断0和极小值的区别,这就会导致模型失败,也就是下溢问题。上溢也是如此,但是这在概率中并不存在,因为数字往往并不会很大,因此通常情况为了避免问题的发生,会对每一个单独的数字进行对数操作,将数字进行转变,防止出现上溢或者下溢操作。当然正常来讲,朴素贝叶斯并不需要这步操作,因为概率不不可能无限趋近于0。
对于类条件概率的求值有两种情况,分别为离散型和连续性,所有的机器学习算法都离不开这两个问题,往往离散型的数据比较容易求解。
1. 离散型,离散型只需要统计个数即可,但是有时为了防止概率0的出现,会对概率进行平滑处理,常用--拉普拉斯修正--来处理这类问题,公式如下所示:
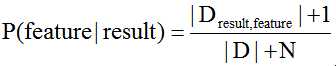
其中D表示所有样本的个数,Dresult,feature表示样本中拥有该特征值且值为result的个数,N表示在该特征值上有多少种情况(类别)。用来保证P(feature|result)的在该特征上的和为1。
2. 连续型,连续型数据考虑概率密度函数,根据在i属性上的均值和方差进行衡量,衡量公式为:

其中均值和方差如下所示:N(μresult,feature,σresult,feature),这里的方差是样本方差,分母是n-1,并不是n,至于原因,知乎解答。
三、半朴素贝叶斯
朴素贝叶斯中最重要的假设就是:属性条件独立性。在现实生活中,往往这个条件很难成立,例如你工资高可能你的消费水平就会适当提升,亦或是家境好,你的消费水平也会受到影响。
所以嘞,尝试去对条件独立性这个条件进行放松,由此产生半朴素贝叶斯的学习方法。
基本思想:适当考虑一部分属性间的相互依赖信息,从而既不需要进行完全联合概率计算,又不至于忽略了比较强的属性依赖关系。
策略:ODE(One-Dependent Estimator)独依赖估计——假设每个属性在类别之外最多依赖一个其他属性。
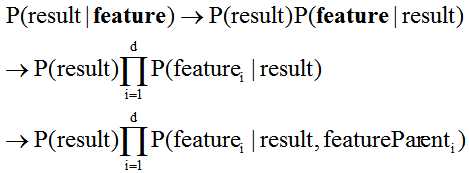
在半朴素贝叶斯分类器中,最主要的问题便是如何确定每个属性的关联属性,换句话讲,也就是父属性。根据不同的确定方法,会产生不同的独依赖分类器。
1. SPODE(Super-Parent ODE)超父独依赖估计
假定所有的属性都依赖于同一个属性(例如都选择属性x1作为父属性),这个属性称作“超父”。通过交叉验证等模型来判断选择父属性。缺点可能不止一点半点。
2. TAN(Tree Augmented naive Bayes)最大带权生成树
a. 计算任意两个属性之间的条件互信息值
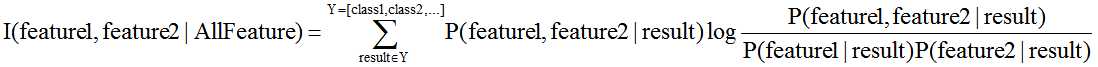
b. 根据所有互信息值构建一个全连通图,任意两个属性之间的权值设定为互信息值
c. 利用Prim算法或者Kurskal算法来得到最大带权生成树
Prim是从某点出发不断找已走结点中到未知结点的最小距离并加入,Kurskal算法是遍历所有边,不断的加入不构成环形结构的节点和边。
Prim适合边多点少的,Kurskal适合点多边少的。
此外扩充下Dijkstra,他是一个求最短路径的算法,如果说Prim是求N个村子如何修路的问题,那么Dijkstra是计算N个村子如何从A村走到其他村庄的最短路径。
d. 确定各自父类
3. AODE(Averaged One-Dependent Estimator)平均独依赖估计
和SPODE不一样的地方在于,AODE尝试将每个属性都作为超父来构建SPODE,然后进行集成作为最终结果。换句话讲,AODE是一种基于集成学习机制、更为强大的独依赖分类器。
具体公式如下所示:
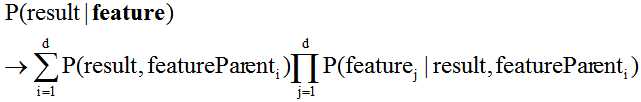
从公式可以看出,和朴素贝叶斯公司类似,AODE的训练过程也是统计概率,然后对符合条件的样本进行计数的过程。公式的具体问题可以根据实际情况进行取舍的哟。
四、贝叶斯网络
1.贝叶斯网络计算
贝叶斯网络也称为信念网(belief network),毕竟贝叶斯网络全靠置信度来进行判断所属类别嘛。
借住DAG(Directed Acyclic Graph)有向无环图——来刻画属性之间的依赖关系,用CPT(Conditional Probability Table)条件概率表来描述属性的联合概率分布。
根据贝叶斯网络可以得到全部的关联关系,根据关联关系,由顶置低的可以获得联合概率分布的结果,图像(贝叶斯网络)可以通过独立关系来表示,独立关系通过文字描述获取,简单来整理如下所示:
文字描述:feature3和feature4在给定feature1的取值时独立,feature4和feature5在给定feature2的取值时独立.
独立关系(公式表达):feature3⊥feature4|feature1 feature4⊥feature5|feature2 (独立结果不止这些,后续会说)
有向无环图:
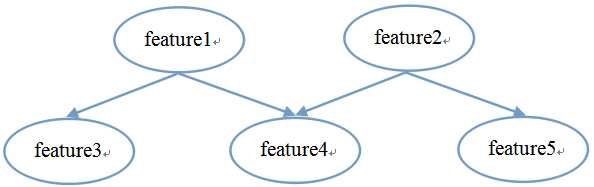
联合概率分布公式:
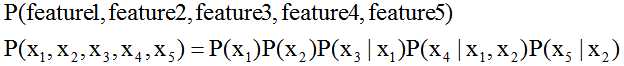
判断独立性的方法,首先将有向无环图中的V型结构(feature1和feature2共同决定feature4)的两个父节点连线,并转换成无向图。如下图所示:
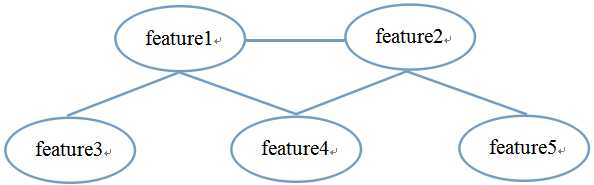
如果特征1和特征2能被特征结合K分开,那么说特征1和特征2是独立的,例如feature2⊥feature3|feature1(上面所说的不止那两个独立情况)。
2. 学习贝叶斯网络图
之前说了那么多都他喵的是废话,怎么搞出来网络结构才是贝叶斯网络的重中之重。
使用“评分搜索”就可以很好地解决问题,设定评分函数,根据此函数评估贝叶斯网络和训练数据的契合程度,基于评分函数寻找最优贝叶斯网络。
a. 选择评分函数
类似于损失函数,我们通常为了让分类更加准确,来让损失函数最小化,在这里,我们选择去让评分函数作为极大似然估计。而无论是AIC(1)还是BIC(1/2logm),归根到底都是求贝叶斯网络的极大似然函数。
极大似然函数:
已知具有某种数据满足某种概率分布,但是具体参数并不知情,通过若干次试验并通过结果推算出参数的大概值。极大似然估计就是建立在这种思想之上,已知某个参数能够让这个样本出现的概率最大,所以干脆把这个参数当做估计的真实值。具体步骤如下:
从所有的网络结构空间中决策出最优贝叶斯网络是一个NP难问题,难以快速求解,大题解决方案有如下两种:
a. 从某个网络出发,每次增删改一条边,直到评分函数的值不在降低为止
b. 施加约束来节省搜索空间,例如将网络限定为树形结构,TAN可看做是贝叶斯网的特例
NP难问题:
推销员旅行问题显然是 NP 的。因为如果你任意给出一个行程安排,可以很容易算出旅行总开销。但是,要想知道一条总路费小于 C 的行程是否存在,在最坏情况下,必须检查所有可能的旅行安排! 这将是个天文数字。
3. 根据贝叶斯网络判断联合概率
通过贝叶斯网中的联合概率分布可以精确的计算后验概率,但是当网络节点较多、连接稠密的时候,难以进行判断。所以需要借助“近似推断”,降低精度的要求,来换取时间上的提升。通常采用——吉布斯采样来完成。
吉布斯采样:一种随机采样方法,随机产生一个和证据变量(也就是我们所说的特征情况)一致的样本作为初始点,然后从当前初始点出发去产生下一个样本。随机初始化待查询变量,对带查询变量逐个进行采样改变其值,采样改变方法根据贝叶斯网络来判定,进行T次,判断有多少次符合我们所要的结果,这个结果便是估算出来的后验概率。
通俗解释:取样就是以一定的概率分布,看发生什么事件。举一个例子。甲只能E:吃饭、学习、打球,时间T:上午、下午、晚上,天气W:晴朗、刮风、下雨。现在要一个样本,这个样本可以是:打球+下午+晴朗。
问题是我们不知道p(E,T,W),或者说,不知道三件事的联合分布joint distribution。当然,如果知道的话,就没有必要用gibbs sampling了。但是,我们知道三件事的conditional distribution。也就是说,p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用gibbs sampling的方法,得到联合分布。
具体方法。首先随便初始化一个组合,i.e. 学习+晚上+刮风,然后依条件概率改变其中的一个变量。具体说,假设我们知道晚上+刮风,我们给E生成一个变量,比如,学习-》吃饭。我们再依条件概率改下一个变量,根据学习+刮风,把晚上变成上午。类似地,把刮风变成刮风(当然可以变成相同的变量)。这样学习+晚上+刮风-》吃饭+上午+刮风。同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
关于MCMC、马尔可夫链之后在整理,现在先知道吉布斯采样就可以了,啧啧。
五、EM算法
训练样本总会有不完整的时候,尤其是你自己去提取数据的时候,对于这种不存在观测值情况下,就会造成训练样本不完整。
未观测变量——隐变量,以下用A表示以观测变量,B表示未观测变量,θ表示模型参数,通过极大似然函数来求解问题:
1. 写出似然函数 P(A,B|θ)
2. 对似然函数取对数并整理 LL(θ|A,B)=ln(P(A,B|θ))
3. B不存在所以对B计算期望LL(θ|A)=ln(P(A|θ))=ln∑BP(A,B|θ),
EM算法——期望最大化算法就是常用的估计参数隐变量的方法,采用迭代的方式,基本步骤如下:
1. E——θ值已知,根据训练数据推断出最优隐变量B的值
2. M——B已知,对参数θ进行极大似然估计
高斯混合聚类的使用的就是EM算法,等聚类的时候在啃,先把这个啃了。
标签:bic 部分 失败 路径 image 贝叶斯定理 准确率 img 导数
原文地址:https://www.cnblogs.com/BloodConey/p/8743981.html