标签:下载 开始 存在 algo dfs else 描述 数据 输入格式
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,?,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
从文件manager.in中读入数据。
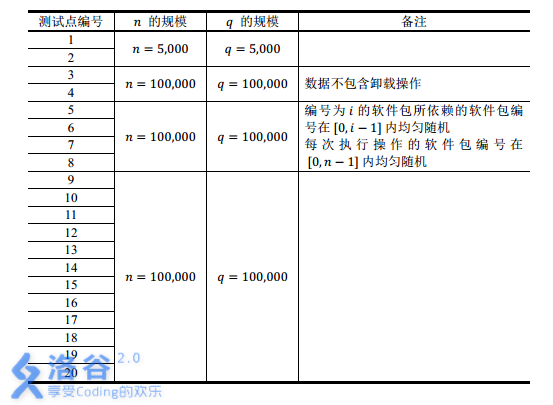
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n?1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,?,n?2,n?1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
【样例说明 1】
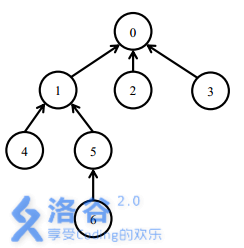
一开始所有的软件包都处于未安装状态。
安装5号软件包,需要安装0,1,5三个软件包。
之后安装6号软件包,只需要安装6号软件包。此时安装了0,1,5,6四个软件包。
卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。
之后安装4号软件包,需要安装1,4两个软件包。此时0,1,4处在安装状态。最后,卸载0号软件包会卸载所有的软件包。`
*********************
题目好长读的好累
对每个软件
他要依赖的软件作为他的父亲连边就得到一棵树
对树上每个节点
权值为1表示已安装,0表示未安装
安装软件包
转化为查询从该节点到根有多少个结点权值为0
那么我们就查询该节点到根的路径和
用该节点深度-路径和得到答案
然后再更新该路径全部置为1
卸载软件包
查询该节点为根的子树总权值和
更新子树全部置为0
一个优化
可以发现每次查询与修改都是同一个区间
那么我们不用分两个函数查询更新
直接同时进行就好,具体见代码
还要注意
每个结点编号都要后移一位
不能让编号存在0
***************************
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
int read()
{
int f=1,x=0;
char ss=getchar();
while(ss<‘0‘||ss>‘9‘){if(ss==‘-‘)f=-1;ss=getchar();}
while(ss>=‘0‘&&ss<=‘9‘){x=x*10+ss-‘0‘;ss=getchar();}
return f*x;
}
void print(int x)
{
if(x<0){putchar(‘-‘);x=-x;}
if(x>9)print(x/10);
putchar(x%10+‘0‘);
}
int n,k;
int tot,cnt;
struct node{int v,nxt;}E[200010];
int head[100010];
int dep[100010],size[100010],fa[100010],top[100010];
int son[100010],num[100010];
int sum[500010],set[500010],orsum[500010];
char ss[20];
void add(int u,int v)
{
E[++tot].nxt=head[u];
E[tot].v=v;
head[u]=tot;
}
void dfs1(int u,int pa)
{
size[u]=1;
for(int i=head[u];i;i=E[i].nxt)
{
int v=E[i].v;
dep[v]=dep[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int tp)
{
top[u]=tp; num[u]=++cnt;
if(son[u]) dfs2(son[u],tp);
for(int i=head[u];i;i=E[i].nxt)
{
int v=E[i].v;
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
void push(int mid,int s,int t,int p)
{
set[p<<1]=set[p<<1|1]=set[p];
if(set[p]==0)sum[p<<1]=sum[p<<1|1]=0;
else sum[p<<1]=mid-s+1,sum[p<<1|1]=t-mid;
set[p]=-1;
}
int getsum(int ll,int rr,int s,int t,int p,int w)
{
if(ll<=s&&t<=rr){int ans=sum[p]; set[p]=w; sum[p]=(t-s+1)*w; return ans;}//先记录答案,在更新,放标记,返回
int mid=s+t>>1;
if(set[p]>=0)push(mid,s,t,p);
int ans=0;
if(ll<=mid) ans+=getsum(ll,rr,s,mid,p<<1,w);
if(rr>mid) ans+=getsum(ll,rr,mid+1,t,p<<1|1,w);
sum[p]=sum[p<<1]+sum[p<<1|1];
return ans;
}
int qsum(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
ans+=getsum(num[top[u]],num[u],1,n,1,1);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
ans+=getsum(num[u],num[v],1,n,1,1);
return ans;
}
int main()
{
n=read();
for(int i=1;i<n;i++)
{
int u=read()+1;
fa[i+1]=u; add(u,i+1);
}
dep[1]=1;
dfs1(1,-1); dfs2(1,1);
memset(set,-1,sizeof(set));
int q=read();
while(q--)
{
scanf("%s",&ss);int u=read()+1,ans;
if(ss[0]==‘i‘)
{
ans=qsum(u,1);
ans=dep[u]-ans;
}
else if(ss[0]==‘u‘)
ans=getsum(num[u],num[u]+size[u]-1,1,n,1,0);
print(ans);printf("\n");
}
return 0;
}标签:下载 开始 存在 algo dfs else 描述 数据 输入格式
原文地址:https://www.cnblogs.com/niiick/p/8746748.html