标签:有助于 通信 share udf ott struct 灯光 需要 答案
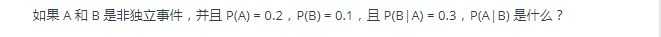
P(A/B)=P(B/A)*P(A)/P(B) 0.3*0.2/0.1

2.全概率公式

3.贝叶斯法则
例子1:你希望得出一辆汽车看见黄色 的交通信号灯就停下来的概率是多少。
经验数据告诉你,一辆汽车在交通灯交叉路口停车的概率是 P(S) = 0.40 。
同时你了解到,基于经验数据,交通灯是黄色(而不是红色或绿色)的概率是 P(Y) = 0.10。

当汽车停在十字路口时,数据显示,灯光为黄色的时间占比为 12%。所以,如果我们知道一辆车停了下来,那么有 12% 的可能性是黄灯。 这被称为条件概率。
给定上面的 P(S) 和 P(Y),如何用符号表示这个条件概率?
P(Y/S)=0.12
如果交通信号灯为黄色,那么汽车停下的可能性0是多少?
P(S/Y)=P(Y/S)*P(S)/P(Y)=0.12*0.4/0.1=0.48
例子2:在一条四车道的高速公路上,汽车行驶速度要么快,要么不快。 快的汽车应该在最左边的车道。
在任何时候,都有 20% 的车辆在最左边的车道。P(左)=0.2
总体上,高速公路上有 40% 的车辆被归类为快速行驶。P(快)=0.4
在最左边车道的所有车辆中,90% 的车辆正在快速行驶。P(快/左)=0.9
如果汽车行驶速度很快,那么它位于最左边车道的概率是多少?
P(左/快)=P(快/左)*P(左)/P(快)=0.9*0.2/0.4=0.45
例子3:
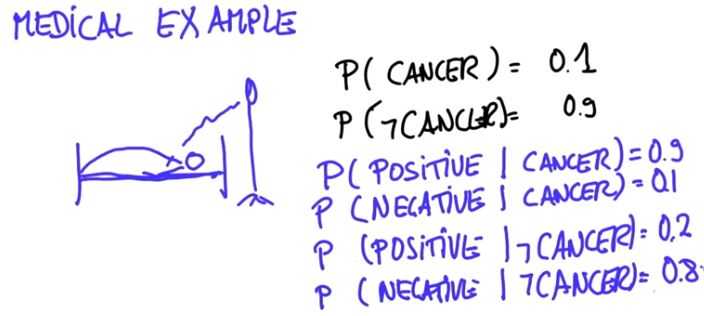
如果一个人的癌症检测结果为阳性,那么他患癌症的概率是多少?
P(癌/阳)=P(阳/癌)*P(癌)/P(阳)=[P(阳/癌)*P(癌)]/[P(阳/癌)*P(癌)+P(阳/正常)*P(正常)]=0.9*0.01/[0.9*0.01+0.05*0.99]
例子4:
了解解决方案的逐步细分很重要。让我们回顾一下解决方案视频中的内容。
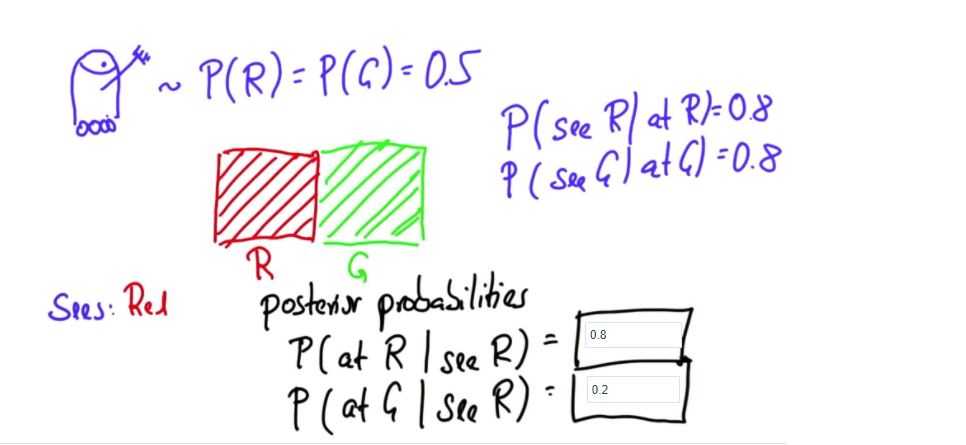
机器人完全不知道自己在哪里,先验概率如下
P(at red)=0.5
P(at green)=0.5
机器人传感器不是十全十美的。 仅仅因为机器人看见 红色,并 不代表 机器人是在红色格子中。
P(see red∣at red)=0.8
P(see green∣at green)=0.8
从先验概率和后验概率中,我们需要计算机器人看见红色之后的后验概率:
P(at red∣see red)
P(at green∣see red)
提示,贝叶斯法则如下所示:
P(A∣B)=P(B∣A)?P(A)?/P(B)
我们可以将贝叶斯法则中的 A 和B 替换掉,显示为:
P(at red∣see red)=P(see red∣at red)?P(at red)?/P(see red)
现在,我们了解先验概率和条件概率后,可以改写为:
P(at red∣see red)=0.8?0.5?/P(see red)
不过我们还不知道一件事!我们看见红色的概率是多少? 答案是 0.5。我可以用两种方式来证明,一是直观预测,二是数学。
当然是 0.5!不然呢? 机器人有 50% 的概率认为自己在红色格子里,有50%的概率认为自己在绿色格子里。当然,它的传感器是不可靠的,但不可靠性是对称的,而不是错误地看到任何一种颜色。 所以无论看到红色的可能性是多少,这也将是看到绿色的可能性。由于这两种颜色是唯一可能的颜色,所以看到每种颜色的概率一定是 50% !
机器人看到红色有以下两种情况。
P(see red)=P(at red)?P(see red∣at red)+P(at green)?P(see red∣at green)
我可以由此得出答案:
P(see red)=0.5?0.8+0.5?0.2
P(see red)=0.4+0.1
P(see red)=0.5
标签:有助于 通信 share udf ott struct 灯光 需要 答案
原文地址:https://www.cnblogs.com/fuhang/p/8758735.html