标签:bsp clu 多个 amp alt gcd 因子 day struct
题目链接 https://files.cnblogs.com/files/lovewhy/P75.pdf
P75
竞赛时间: ????年??月??日??:??-??:??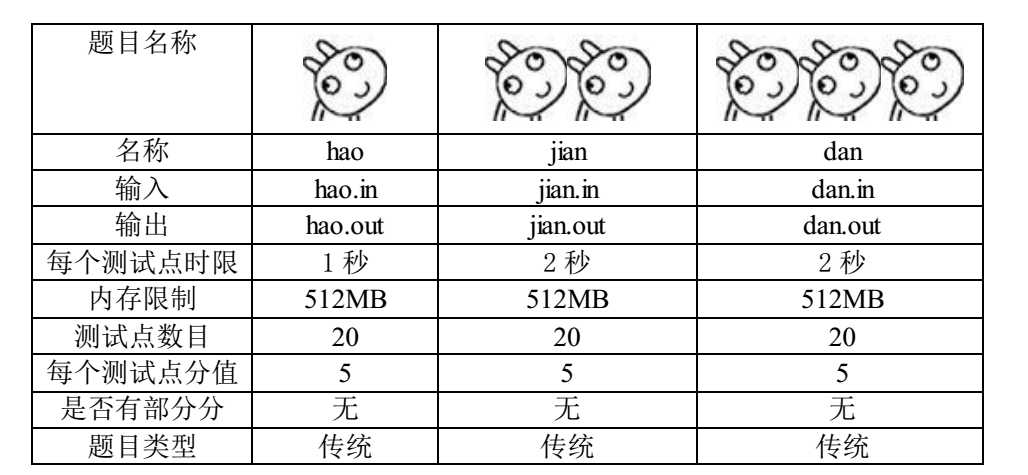
注意事项(请务必仔细阅读)
T1
【 问题描述】
从1 ? N中找一些数乘起来使得答案是一个完全平方数,求这个完全平方数
最大可能是多少。
【输入格式】
第一行一个数字N。
【输出格式】
一行一个整数代表答案对100000007取模之后的答案。
【样例输入】
7
【样例输出】
144
【样例解释】
但是塔外面有东西。
【数据规模与约定】
对于20%的数据, 1 ≤ N ≤ 100。
对于50%的数据, 1 ≤ N ≤ 5000。
对于70%的数据, 1 ≤ N ≤ 10^5。
对于100%的数据, 1 ≤ N ≤ 5 × 10^6。
//数学题2333 //竟然考了数学题mmp //果然翻车了 //T1一分也没有 //数论是个大坑,埋葬了我 //把n!分解质因数,记录质因子出现的个数 //如果某个质因子a出现了偶数次,假设是b次,那么它就可以由a^(b/2) * a^(b/2)得到, //也就是说,只要这个质因子出现了偶数次,它就组成了一个完全平方数 //如果多个质因子出现了偶数次,同理,他们也可以都分成两半再乘起来得到 //如果是奇数呢? //那就丢一个,使其变成偶数次 #include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const int mod=1e8+7; const int N=5e6+5; int n; int tot[N]; int prime[N],cnt; bool nprime[N]; inline int read() { char c=getchar();int num=0; for(;!isdigit(c);c=getchar()); for(;isdigit(c);c=getchar()) num=num*10+c-‘0‘; return num; } inline void init() { long long tmp; for(int i=2;i<=n;++i) { if(!nprime[i]) prime[++cnt]=i; for(int j=1;j<=cnt;++j) { tmp=1ll*prime[j]*i; if(tmp>n) break; nprime[tmp]=1; if(i%prime[j]==0) break; } } } long long ksm(long long a,long long k) { long long Ans=1; while(k) { if(k&1) Ans=Ans*a,Ans%=mod; k>>=1; a*=a; a%=mod; } return Ans; } inline void work() { for(int i=1;i<=cnt;++i) { int tmp=n; while(tmp) { tot[i]+=tmp/prime[i]; tmp/=prime[i]; } } } int main() { n=read(); init(); work(); long long ans=1; for(int i=1;i<=cnt;++i) { ans*=1ll*ksm(prime[i],tot[i]/2*2); ans%=mod; } printf("%lld",ans); return 0; }
T2
【问题描述】
有N个数,随机选择一段区间,如果这段区间的所有数的平均值在[??, ??]中则你比较厉害。求你比较厉害的概率。
【输入格式】
第一行有三个数N, l, r,含义如上描述。
接下来一行有N个数代表每一个数的值。
【输出格式】
输出一行一个分数a/b代表答案,其中a, b互质。 如果答案为整数则直接输出该
整数即可。
【样例输入 1】
4 2 3
3 1 2 4
【样例输出 1】
7/10
【样例输入 2】
4 1 4
3 1 2 4
【样例输出 2】
1
【样例解释】
塔外面有棵树。
【数据规模与约定】
对于30%的数据, 1 ≤ N ≤ 104。
对于60%的数据, 1 ≤ N ≤ 105。
对于100%的数据, 1 ≤ N ≤ 5 × 105, 0 < l ≤ r ≤ 100。

//T2... //想想。。。它什么时候不如我们厉害呢? //就是平均值不在[l,r]呗。。。。 //,,....mmp //没点赫拉克勒斯。 //ei?突然发现T2两秒时限 //不知道能不能n^2过30分 #include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int N=5e5+5; int n,l,r; int sum[N]; int fenmu,fenzi; inline int read() { char c=getchar();int num=0,f=1; for(;!isdigit(c);c=getchar()) f=c==‘-‘?-1:f; for(;isdigit(c);c=getchar()) num=num*10+c-‘0‘; return num*f; } int gcd(int x,int y) { int tmp; while(y) { tmp=x; x=y; y=tmp%y; } return x; } int main() { freopen("jian.in","r",stdin); freopen("jian.out","w",stdout); n=read(),l=read(),r=read(); if(n<=10000) { for(int i=1,a;i<=n;++i) { a=read(); sum[i]=sum[i-1]+a; // cout<<sum[i]<<" "; } // cout<<endl; fenmu=n*(n+1)>>1; // cout<<"fenmu: "<<fenmu<<‘\n‘; int num,len; for(int i=1;i<=n;++i) { for(int j=i;j<=n;++j) { num=sum[j]-sum[i-1]; len=j-i+1; if(num>=l*len&&num<=r*len) ++fenzi; } } if(!fenzi) puts("0"); else if(fenzi==fenmu) puts("1"); else { int g=gcd(fenzi,fenmu); printf("%d/%d",fenzi/g,fenmu/g); } } else puts("0"); fclose(stdin); fclose(stdout); return 0; }
T3
【问题描述】
m × m的方阵上有n棵葱, 你要修一些栅栏把它们围起来。 一个栅栏是一段
沿着网格建造的封闭图形( 即要围成一圈)。 各个栅栏之间应该不相交、 不重叠
且互相不包含。 如果你最多修k个栅栏, 那么所有栅栏的长度之和最小是多少?
【 输入格式】
第一行三个整数m, k, n。
接下来n行每行两个整数x, y代表某棵葱的位置。
【 输出格式】
一行一个整数代表答案。
【样例输入 1】
6 1 4
1 3
4 2
4 4
6 4
【 样例输出 1】
18
【样例输入 2】
6 2 4
1 3
4 2
4 4
6 4
【 样例输出 2】
16
【 样例解释】
你猜树上有啥。
【数据规模与约定】
对于10%的数据, k = 1。
对于30%的数据, k ≤ 2。
对于60%的数据, n ≤ 10。
对于100%的数据, 1 ≤ k ≤ n ≤ 16, m ≤ 1000。
暴力是冲着30分去的,但是竟然有50分2333

//显然的是,如果是围多棵葱的话,那么直接在外围围的长度==拐弯围的长度 //给这些葱按坐标排个序 //长度等于((x0-x1+1)+(y0-y1+1))*2 #include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<ctime> #define A lb[i].dax #define B lb[i].xiaox #define C lb[i].day #define D lb[i].xiaoy using std::min; using std::max; using std::sort; const int N=1e3+5; const int INF=0x7f7f7f7f; int m,k,n; struct LB { int xiaox,xiaoy,dax,day; }lb[20]; struct CONG { int x,y; }cong[N]; inline int read() { char c=getchar();int num=0; for(;!isdigit(c);c=getchar()); for(;isdigit(c);c=getchar()) num=num*10+c-‘0‘; return num; } int a,b; int Ans,tmp; void dfs(int now) { if(now==n+1) { tmp=0; for(int i=1;i<=k;++i) { if(A) { tmp+=((A-B+1)+(C-D+1))*2; if(tmp>=Ans) return; } } Ans=min(Ans,tmp); return; } for(int i=1;i<=k;++i) { int a1=A,a2=B,a3=C,a4=D; A=max(A,cong[now].x); B=min(B,cong[now].x); C=max(C,cong[now].y); D=min(D,cong[now].y); dfs(now+1); A=a1,B=a2,C=a3,D=a4; } } int main() { freopen("dan.in","r",stdin); freopen("dan.out","w",stdout); if((k<=5&&n<=10)||k==1||k==2) { m=read(),k=read(),n=read(); for(int i=1;i<=n;++i) cong[i].x=read(),cong[i].y=read(); Ans=INF; for(int i=1;i<=k;++i) B=D=INF; dfs(1); printf("%d",Ans); } else { srand(time(NULL)); printf("%d",rand()%101+1); } fclose(stdin); fclose(stdout); return 0; } /* 1000 3 16 1 65 142 455 123 456 545 848 748 132 877 1000 746 712 416 745 786 136 456 452 413 748 13 11 45 485 132 748 412 44 32 453 1 1 */ /* 1000 2 16 1 65 142 455 123 456 545 848 748 132 877 1000 746 712 416 745 786 136 456 452 413 748 13 11 45 485 132 748 412 44 32 453 1 1 */
只加卡时有60分,把if(now==n+1)里的计算拿到外边当了剪枝之后,可以达到95分了!!23333+1
但是在luogu上只能卡到80分。。。。
clock真好用!

//显然的是,如果是围多棵葱的话,那么直接在外围围的长度==拐弯围的长度 //给这些葱按坐标排个序 //长度等于((x0-x1+1)+(y0-y1+1))*2 #include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<ctime> #define A lb[i].dax #define B lb[i].xiaox #define C lb[i].day #define D lb[i].xiaoy using std::min; using std::max; using std::sort; const int N=1e3+5; const int INF=0x7f7f7f7f; int m,k,n; struct LB { int xiaox,xiaoy,dax,day; }lb[20]; struct CONG { int x,y; }cong[N]; inline int read() { char c=getchar();int num=0; for(;!isdigit(c);c=getchar()); for(;isdigit(c);c=getchar()) num=num*10+c-‘0‘; return num; } int a,b; int Ans,tmp; void dfs(int now) { if(clock()>19980) { printf("%d",Ans); exit(0); } tmp=0; for(int i=1;i<=k;++i) { if(A) { tmp+=((A-B+1)+(C-D+1))*2; if(tmp>=Ans) return; } } if(now==n+1) { Ans=tmp; return; } for(int i=1;i<=k;++i) { int a1=A,a2=B,a3=C,a4=D; A=max(A,cong[now].x); B=min(B,cong[now].x); C=max(C,cong[now].y); D=min(D,cong[now].y); dfs(now+1); A=a1,B=a2,C=a3,D=a4; } } int main() { // freopen("dan.in","r",stdin); // freopen("dan.out","w",stdout); if((k<=5&&n<=10)||k==1||k==2) { m=read(),k=read(),n=read(); for(int i=1;i<=n;++i) cong[i].x=read(),cong[i].y=read(); Ans=INF; for(int i=1;i<=k;++i) B=D=INF; dfs(1); printf("%d",Ans); } else { srand(time(NULL)); printf("%d",rand()%101+1); } fclose(stdin); fclose(stdout); return 0; } /* 1000 3 16 1 65 142 455 123 456 545 848 748 132 877 1000 746 712 416 745 786 136 456 452 413 748 13 11 45 485 132 748 412 44 32 453 1 1 */ /* 1000 2 16 1 65 142 455 123 456 545 848 748 132 877 1000 746 712 416 745 786 136 456 452 413 748 13 11 45 485 132 748 412 44 32 453 1 1 */
标签:bsp clu 多个 amp alt gcd 因子 day struct
原文地址:https://www.cnblogs.com/lovewhy/p/8763110.html