标签:原因 单位 另一个 com src 连续 image idt nbsp
以离散信号为例,连续信号同理。
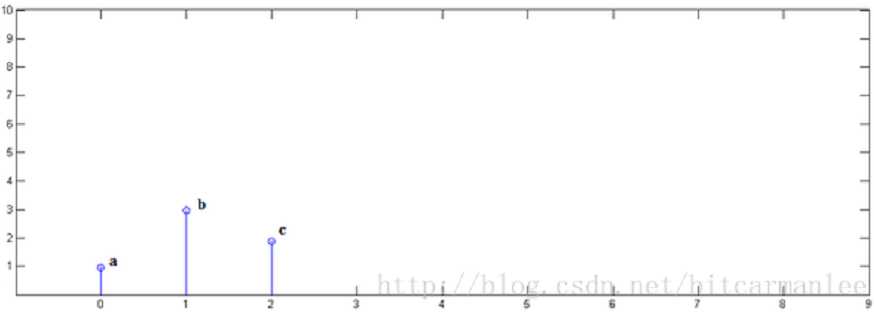
已知 x[0] = a, x[1] = b, x[2]=c
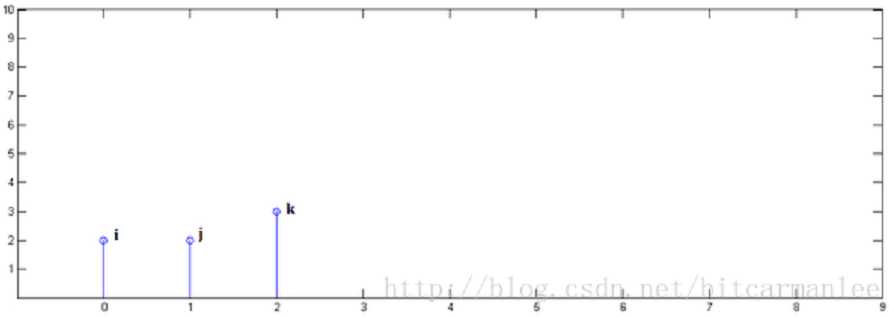
已知 y[0] = i, y[1] = j, y[2]=k
下面通过演示求 x[n] * y[n]的过程,揭示卷积的物理意义。
第一步,x[n]乘以 y[0]并平移到位置 0:
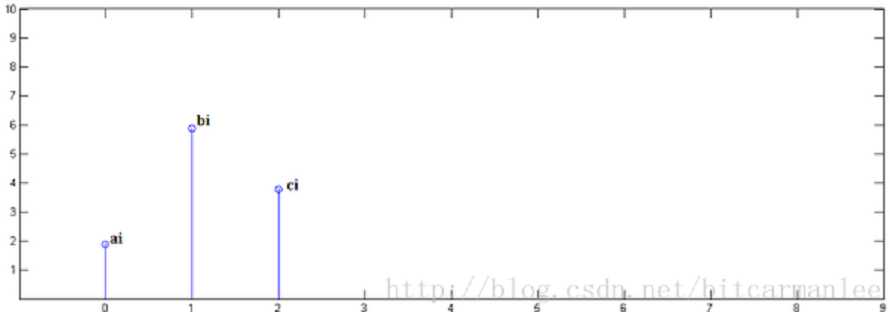
第二步,x[n]乘以 y[1]并平移到位置 1:
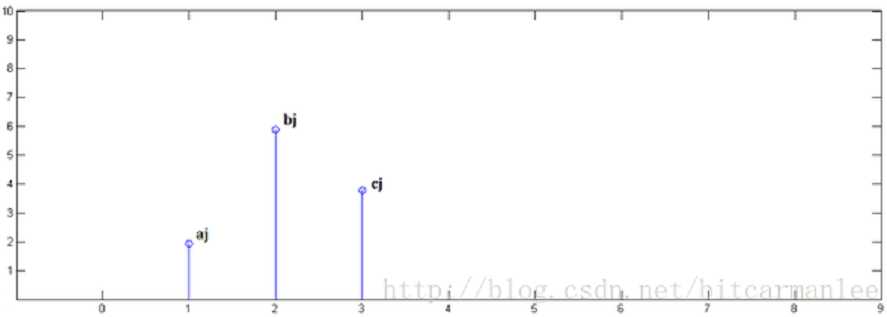
第三步,x[n]乘以 y[2]并平移到位置 2:
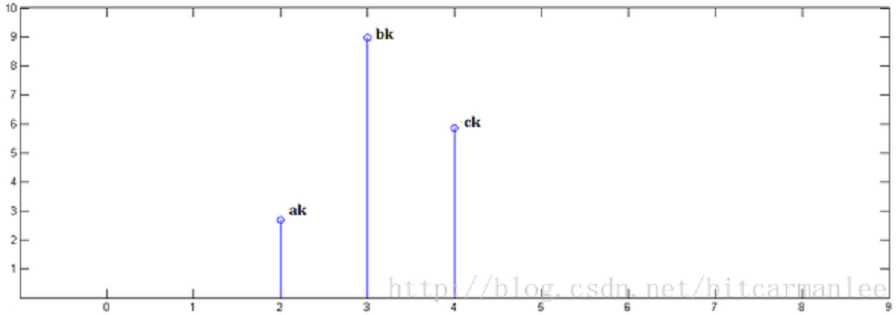
最后,把上面三个图叠加,就得到了 x[n] * y[n]:
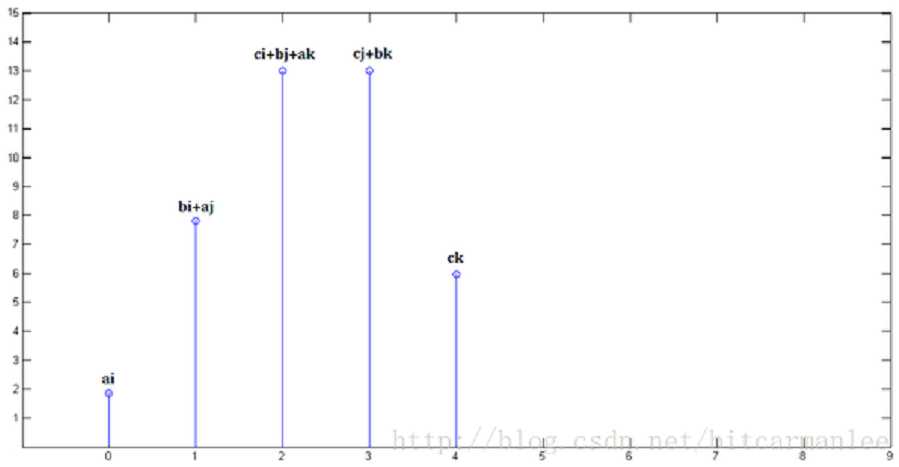
简单吧?无非是平移(没有反褶!)、叠加。
从这里,可以看到卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数
(如:输入信号)上的加权叠加。
重复一遍,这就是卷积的意义:加权叠加。
对于线性时不变系统,如果知道该系统的单位响应,那么将单位响应和输入信号求卷积,
就相当于把输入信号的各个时间点的单位响应 加权叠加,就直接得到了输出信号。
通俗的说:
在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。
这正是单位响应是如此重要的原因。这种做法和通常教材上的区别在于:书上先反褶再平移,把输入信号当作一个整体,一次算出一个时间点的响应值;而楼主把信号拆开,一次算出一个信号在所有时间的响应值,再把各个信号相加。两者本质上是相同的。
卷积的另外解释
卷积表示为 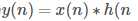
标签:原因 单位 另一个 com src 连续 image idt nbsp
原文地址:https://www.cnblogs.com/2008nmj/p/8778425.html