标签:序号 约束 cin == png font 存在 space type
题目链接:
https://vjudge.net/problem/POJ-3169
题目大意:
一些母牛按序号排成一条直线。有两种要求,A和B距离不得超过X,还有一种是C和D距离不得少于Y,问可能的最大距离。如果没有输出-1,如果可以随便排输出-2,否则输出最大的距离。
Sample Input
4 2 1
1 3 10
2 4 20
2 3 3
Sample Output
27
思路:
设xi为第i头牛的x坐标
对于第一种要求,A和B之间距离不超过X(题目中A<B)
那就有:xB - xA <= X
对于第二种要求,A和B之间距离少于X(题目中A<B)
那就有:xB - xA >= X
对于上述两种不等式,可知这道题就是一堆不等式组,可以用差分约束系统来做。
u是起点,v是终点
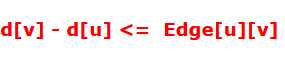
对于第一种不等式,转化成A->B的边,权值为X
对于第二种不等式,先转化成上述形式,xA - xB <= -X,转化成B->A的边,权值是-X
在题目中隐含了一组不等式xi-1<=xi,转化成上述形式就是xi-1 - xi <= 0,边为i -> i-1权值是0
然后要看题目中求的是什么:
求的是从1到n的最大距离
就等价于xn-x1最大
等价于xn-x1 <= M需要求M的最小值(因为M没有最大值,最大值是正无穷)
这个不等式就是1到n的边,权值为M,说明题目求的是1到n的最短路,如果存在负环,输出-1,如果是INF输出-2,否则输出最短路长度。分析到这里就可以套模板啦
1 #include<iostream> 2 #include<vector> 3 #include<queue> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdio> 7 using namespace std; 8 typedef pair<int, int> Pair; 9 const int maxn = 25000 + 10; 10 const int INF = 0x3f3f3f3f; 11 int T, n, m, m1, m2; 12 struct edge 13 { 14 int u, v, w; 15 edge(int u, int v, int w):u(u), v(v), w(w){} 16 edge(){} 17 }; 18 edge e[maxn]; 19 int d[1005], tot; 20 void addedge(int u, int v, int w) 21 { 22 e[tot++] = edge(u, v, w); 23 } 24 bool Bellman() 25 { 26 int u, v, w; 27 memset(d, INF, sizeof(d)); 28 d[1] = 0; 29 for(int j = 0; j < n; j++) 30 { 31 for(int i = 0; i < tot; i++) 32 { 33 u = e[i].u, v = e[i].v, w = e[i].w; 34 if(d[u] < INF && d[v] > d[u] + w) 35 { 36 d[v] = d[u] + w; 37 if(j == n - 1)return true;//存在负环,方程组无解 38 } 39 } 40 } 41 return false; 42 } 43 int main() 44 { 45 cin >> n >> m1 >> m2; 46 int u, v, w; 47 for(int i = 0; i < m1; i++)//第一组边,u->v 权值w 48 { 49 scanf("%d%d%d", &u, &v, &w); 50 addedge(u, v, w); 51 } 52 for(int i = 0; i < m2; i++)//第二组边 v->u 权值-w 53 { 54 scanf("%d%d%d", &u, &v, &w); 55 addedge(v, u, -w); 56 } 57 for(int i = 1; i < n; i++)//第三组边 i+1->i 权值0 58 addedge(i + 1, i, 0); 59 if(Bellman()) 60 { 61 cout<<"-1"<<endl; 62 } 63 else 64 { 65 if(d[n] == INF)cout<<"-2"<<endl; 66 else cout<<d[n]<<endl; 67 } 68 /*for(int i = 1; i <= n; i++) 69 { 70 cout<<i<<":::"; 71 for(int j = 0; j < G[i].size(); j++)cout<<G[i][j].v<<"-"<<G[i][j].w<<" "; 72 cout<<endl; 73 }*/ 74 }
POJ-3169 Layout---差分约束系统+Bellman
标签:序号 约束 cin == png font 存在 space type
原文地址:https://www.cnblogs.com/fzl194/p/8798507.html