标签：标准   一个   aik   margin   lan   分享   影响   style   body   

 一.状态估计的解释

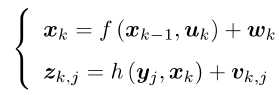
我们知道每个方程都受噪声的影响，这里把位姿x和路标y看成服从某种概率分布的随机变量。因此我们关心的问题就变成了：当我们已知某些运动数据u和观测数据z时，如何确定状态量x，y的分布？比较常见且合理的情况下，我们假设状态量和噪声项服从高斯分布---这意味着在程序中只需存储它们的均值和协方差即可。均值可看作是对变量最优值的估计，而协方差矩阵度量了它的不确定性。如果认为k时刻状态只与k-1时刻状态有关，而与再之前无关，我们就会得到以卡尔曼滤波（EKF）为代表的滤波器方法，在滤波方法综合那个，我们会将某时刻的状态估计，推导到下一时刻；另一种方法考虑k时刻状态与之前所有状态的关系，将得到以非线性优化为主体的优化框架。目前SLAM的主流是非线性优化方法。

二.EKF

卡尔曼滤波 -- 从推导到应用(一)

卡尔曼滤波 -- 从应用(一) 到 (二)

高斯分布，又称为正态分布 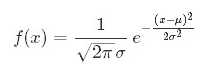    正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

后端---EKF+非线性优化

标签：标准   一个   aik   margin   lan   分享   影响   style   body   

原文地址：https://www.cnblogs.com/Jessica-jie/p/8806816.html