标签：none form rom path data 排序 space sed XA
5
3 2 2 3 3
Possible
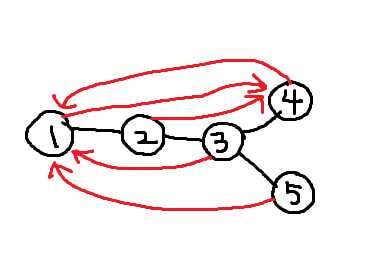
The diagram above shows an example of a tree that satisfies the conditions. The red arrows show paths from each vertex to the farthest vertex from it.
解析
代码比较长，整体思路就是先排序，找到最长的那一路，然后确定这个长度为主干（比如说最长的是n，那主干长度是n+1），然后把其他的分支都可以插在中间，但是这些分路构成的长度不能长于主干长度，因此这些分支的距离就是主干中间的最长距离加一，就比如说样例，主干长度是3，因此有4个数为主干，因此这四个数的最长距离为3、2、2、3，剩下的一个可以在中间的两个二中任选一个加一，就是3、2、2、3、3。
#include <bits/stdc++.h> using namespace std; typedef long long ll; int s[200]; int main() { ios::sync_with_stdio(false); int i,j,k,m,n; int ans=0,cnt=0; int flag=0; int flag1=0; cin>>n; for(i=1; i<=n; i++) cin>>s[i]; sort(s+1,s+n+1); int gen=s[n],num=0; for(i=1; i<=n; i++) if(s[i]==gen) num++; if(num==1) cout<<"Impossible"<<endl; else { if(gen%2!=0) { k=(gen+1)/2; m=k; for(i=1;i<=n;i++) { if(s[i]==k) { cnt++; } if(cnt>2) { cout<<"Impossible"<<endl; return 0; } } for(i=1; i<=n; i++) { if(s[i]<k) { cout<<"Impossible"<<endl; return 0; } if(m==s[i]) { ans++; } if(ans==2) { ans=0; m++; } if(m==(gen+1)) { cout<<"Possible"<<endl; return 0; } } cout<<"Impossible"<<endl; } else { k=gen/2; m=k; for(i=1;i<=n;i++) { if(s[i]==k) { cnt++; } if(cnt>1) { cout<<"Impossible"<<endl; return 0; } } for(i=1; i<=n; i++) { if(s[i]<k) { cout<<"Impossible"<<endl; return 0; } if(m==s[i]) { ans++; } if(ans==2&&flag) { ans=0; m++; } else if(ans==1&&!flag) { ans=0; m++; flag=1; } if(m==gen+1) { cout<<"Possible"<<endl; return 0; } } cout<<"Impossible"<<endl; } } return 0; }
标签：none form rom path data 排序 space sed XA
原文地址：https://www.cnblogs.com/nublity/p/8811293.html
