标签:bool 算数运算 line return and hash 和我 超过 i++
hash:
把复杂问题映射到一个容易维护的值域, 因为值域变简单, 范围变小, 可能会造成两个不同的值被hash函数映射到同一个值上,因此需要处理冲突情况
开散列:建立一个邻接表结构,以hash函数的值域作为表头数组head, 映射后的值相同的原始信息被分在同一类, 构成一个链表接在对应的表头, 链表的节点保存原始信息和统计数据(大概就是拉链式hash??)
hash的两个基本操作
1.计算hash函数的值
2.定位到对应链表依次遍历,比较
例:我们要在一个长度为n的随机整数序列A中统计每个数出现了多少次
一般思路:
直接数组计数
hash思路:
设计一个hash函数为h(x) = (x mod p) + 1, 其中p是一个比较大的质数, 但不超过n。这样,显然,我们把数列A分成了P类, 我们依次考虑数列中的每个数A[i], 定位到hash[h(A[i])]这个表头所指向的链表,如果该链表不包含A[i], 我们就在尾部新插入一个节点A[i], 并在该节点上记录A[i]出现了1次,否则直接找到已经存在的节点A[i],并将其出现次数+1。因为整数序列A是随机的,所以最终所以A[i]会比较均匀的分散在各个表头,整个算法的复杂度接近O(n)
对于非随机数列,我们可以设计更好的hash函数来保证其时间复杂度。同样的,如果我们需要维护的是比大整数复杂得多的某些性质(如是否存在,出现次数),也可以通过hash解决
emmmm....放一道基本水题感受下:
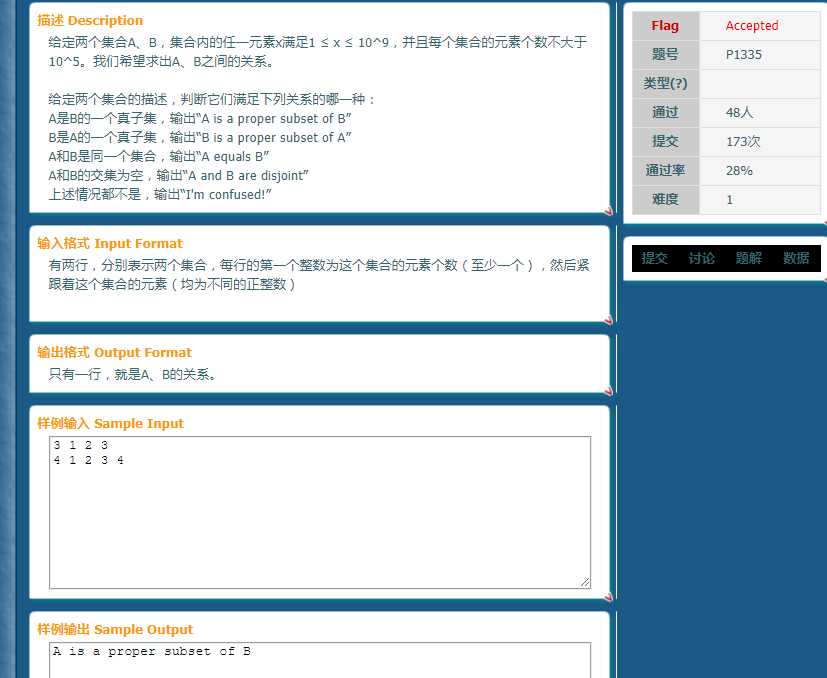
emmmm要是x小一点就可以丢到数组那当基本题了,然而很大,显然要是直接用数组会爆内存,所以我们来hash吧,这之后的问题解决就是数学的集合的事情了
丢份丑陋的代码:
#include <bits/stdc++.h> #define p 2323237 using namespace std; struct node { int v, next, num; }hash[p]; int n, sum = 0, a, b, bsum = 0; int lin[p], len = 0; bool flag1 = 0, flag = 0; inline int read() { int x = 0, y = 1; char ch = getchar(); while(!isdigit(ch)) { if(ch == ‘-‘) y = -1; ch = getchar(); } while(isdigit(ch)) { x = (x << 3) + (x << 1) + ch - ‘0‘; ch = getchar(); } return x * y; } inline int getkey(int k) { return k % p;} inline void insert(int key, int v) { hash[++len].next = lin[key]; hash[len].v = v; hash[len].num = 1; lin[key] = len; } inline void hash_(int k, int c) { int key = getkey(k); if(c == 1) insert(key, k); else { for(int i = lin[key]; i; i = hash[i].next) if(hash[i].v == k) { hash[i].num++; flag1 = 1; flag = 1; sum++; } if(flag == 0) { insert(key, k); bsum++; } flag = 0; } } int main(){ for(int i = 1; i <= 2; i++) { n = read(); int x; if(i == 1) a = n; else b = n; for(int j = 1; j <= n; j++) { x = read(); hash_(x, i); } } if(!flag1) cout << "A and B are disjoint" << endl; else { if(bsum == 0) { if(sum == a) cout << "A equals B" << endl; else cout << "B is a proper subset of A" << endl; } else if(bsum != 0) { if(sum == a) cout << "A is a proper subset of B" << endl; else cout << "I‘m confused!" << endl; } } return 0; }
字符型hash
字符型hash,即把一个任意长度的字符映射成一个非负整数,并且冲突概率几乎为0
取一固定值P,把字符串看做P进制数,并分配一个大于0的数值, 代表每种字符。 一般来说, 我们分配的数值都远小于P, 例如对于小写字母构成的字符串,可以令:a = 1, b = 2, c = 3, .....z = 26。取一固定值M,将P对M取模,作为该字符的hash值 。
一般的说,我们取P = 131或P = 13331, 此时产生冲突的概率极低,只要hash值相同,我们就可以认为原字符串相等的。但是现实是,我们最好还是直接比较字符串是否相同,不然很容易就挂了.jpg,同样拉链式hash很重要.jpg,不然活该被卡(来自被花式卡死的人的怨念。)
一般我们采用M = 2^64, 即直接使用unsigned long long 类型存储hash值, 在计算时产生算术溢出时相当于直接的2^64取%, 这样可以避免低效的取%运算.jpg
我们也可以多取一些恰当的P和M的值(例如一些大质数,就比如如果你的企鹅号是质数...),多进行几组hash运算,当结果都相同时才认为与原字符串相等,一般来说,再毒瘤的出题人也很难构造出使这个hash产生错误的数据了,如果不行还是挂了,呵呵,出题人这辈子怕是没有rp了。但是如果你只运行1次,emmm,不被卡才怪。
对于字符串的各种操作,可以直接对P进制数进行算数运算反映到hash上
比如我们已知一个字符串S的hash值为Hash(S), 那么在S后添加一个字符c构成新字符S + c的hash值就是
Hash(S + c) = (Hash(S) * P + value[c]) % M。其中乘P相当于P进制下的左移运算, value数组是我们预先处理的字母的映射数组, value[c]就是我们选定的c的代表数值。
再如我们已知字符串S的hash值为Hash(S), 字符串S + T的hash值为Hash(S + T),那么字符串T的hash值
Hash(T) = (Hash(S + T) - Hash(S) * P^length(T)) % M
其中 Hash(S) * P^length(T)相当于把Hash(S)在P进制下再S后补0的方式进行算术左移,是S的左端与S + T的左端对齐,这样进行相减后得到的就是字符串T的hash值Hash(T)
例如: S = "abc", c = "d", T = "xyz", value["a, b, c.....z"] = {1, 2, 3, ....26}
S表示为P进制数为1 2 3
Hash(S) = 1 * P^2 + 2 * P + 3
Hash(S + c) = Hash(S) * P + value[c] = (1 * P^2 + 2 * P + 3) * P + 4 = 1 * P^3 + 2 * P^2 + 3 * P + 4
S + T表示为P进制数为1 2 3 24 25 26
Hash(S + T) = 1 * P^5 + 2 * P^4 + 3 * P^3 + 24 * P^2 + 25 * P + 26
Hash(S) * P^length(T) = (1 * P^2 + 2 * P + 3) * P^3 = 1 * P^5 + 2 * P^4 + 3 * P^3
即Hash(S) * P^length(T)表示为P进制数为 1 2 3 0 0 0
显然相减以后我们就得到了T的hash值
即Hash(T) = 1 * P^5 + 2 * P^4 + 3 * P^3 + 24 * P^2 + 25 * P + 26 - (1 * P^5 + 2 * P^4 + 3 * P^3)
表示为P进制数为 1 2 3 24 25 26 - 1 2 3 0 0 0 = 24 25 26
也就是说运算出来的Hash(T)表示为P进制数为24 25 26
Hash(T) = 24 * P^2 + 25 * P + 26
根据以上两种操作,我们可以通过O(n)的时间预处理字符串甚至所有前缀Hash值,并在O(1)的时间内查询任意子串的hash值
丢一道题:
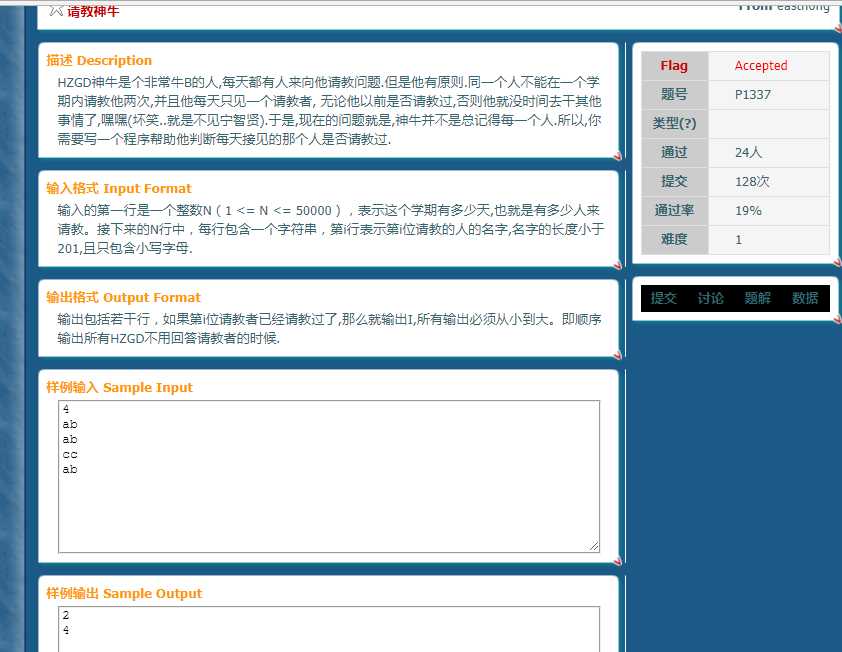
emmm字符串hash,然而切记不要去比较什么hash值,直接比较原字符,顺便把拉链式用上
不然你就会和我一样,WA掉这道题
日常丢代码(emmm刚刚发现博客园是可以插入代码的)
#include <bits/stdc++.h> #define maxn 500086 #define p 131 #define m 2323237 #define ull unsigned long long using namespace std; struct node { char c[510]; int next; }hash[50010]; char ch[maxn]; int ans[maxn], top = 0; int n; int lin[3000010], le = 0; inline void insert(int key) { hash[++le].next = lin[key]; strcpy(hash[le].c, ch); lin[key] = le; } inline void hash_(int k, int c) { register bool flag = 0; for(register int i = lin[k]; i; i = hash[i].next) if(strcmp(hash[i].c, ch) == 0) { ans[++top] = c; flag = 1; cout << c << "\n"; } if(!flag) insert(k); } int main() { ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); cin >> n; for(register int i = 1; i <= n; ++i) { cin >> ch; register int len; register ull key = 0; len = strlen(ch); for(register int j = 0; j < len; ++j) { register int h = ch[j] - ‘a‘ + 1; key = (key * p + h) % m; } hash_(key, i); } return 0; }
标签:bool 算数运算 line return and hash 和我 超过 i++
原文地址:https://www.cnblogs.com/ywjblog/p/8822747.html