标签:color ima 建立 距离 数字 src 多个 max ios
设有一棵二叉树,如图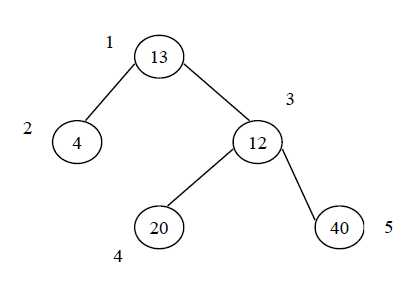
其中,圈中数字表示结点居民的人口.圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻结点之间的距离为1.如上图中,若医院建在:
1 处:则距离之和=4+12+2*20+2*40=136
3 处:则距离之和=4*2+13+20+40=81
…….
输入:
第一行一个整数n,表示树的结点数。(n<=100)
接下来的n 行每行描述了一个结点的状况,包含三个整数,整数之间用空格(一个或多个)分隔,其中:第一个数为居民人口数;第二个数为左链接,为0 表示表链接;第三个数为右链接。
输出:
一个整数,表示最小距离和。
样例输入:
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
样例输出:
81
这道题刚开始我还以为是树形dp,于是菜鸡的我心中一慌。这时我突然发现了感人的数据范围 n <= 100,那不就是啥暴力都能过吗!!!
于是我们枚举每一个点,然后每一次都求一个距离和,最后取所有方案中的最小的。
更为感人的是,边权全都是1,那么我们就可以忘掉各种最短路算法,跑一遍bfs(dfs) 距离和就求出来了。因为点 i 到源点的就离就是从源点走到 i 的步数。
#include<cstdio> #include<algorithm> #include<cmath> #include<cstring> #include<iostream> #include<queue> #include<vector> using namespace std; typedef long long ll; const int maxn = 1e3 + 5; int cost[maxn], v[maxn][3], n; int ans = 1000000; struct Node { int id, step; }; bool vis[maxn]; int bfs(int s) { memset(vis, 0, sizeof(vis)); int sum = 0; queue<Node> q; q.push((Node){s, 0}); vis[s] = 1; while(!q.empty()) { Node now = q.front(); q.pop(); for(int i = 0; i <= 2; ++i) if(v[now.id][i] && !vis[v[now.id][i]]) { vis[v[now.id][i]] = 1; int nstep = now.step + 1; sum += nstep * cost[v[now.id][i]]; q.push((Node){v[now.id][i], nstep}); } } return sum; } int main() { freopen("hospital.in", "r", stdin); freopen("hospital.out", "w", stdout); scanf("%d", &n); for(int i = 1; i <= n; ++i) { int a, b; scanf("%d%d%d", &cost[i], &a, &b); if(a) {v[i][0] = a; v[a][2] = i;} //不喜欢邻接矩阵,用vector存图 if(b) {v[i][1] = b; v[b][2] = i;} } for(int i = 1; i <= n; ++i) ans = min(ans, bfs(i)); printf("%d\n", ans); return 0; }
标签:color ima 建立 距离 数字 src 多个 max ios
原文地址:https://www.cnblogs.com/mrclr/p/8824805.html